${\rm sin}15^\circ=\dfrac{\sqrt{6}-\sqrt{2}}{4}\\{\rm cos}15^\circ=\dfrac{\sqrt{6}+\sqrt{2}}{4}\\ {\rm tan}15^\circ=\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}}=2-\sqrt{3}$
$\sin18^{\circ}=\dfrac{\sqrt{5}-1}{4}$
正の整数の約数の総和を表す公式を二つ紹介します。一つ目は入試でも頻出の必須公式です。
二つ目はコサインとか出てくる観賞用の公式です。玄人向け。
二つ目はコサインとか出てくる観賞用の公式です。玄人向け。
三角錐，四角錐，円錐などの錐体の体積は
$\dfrac{1}{3}$ ×底面積×高さ
誕生日のパラドックス：$23$ 人いれば，その中に同じ誕生日である二人組が $50\%$以上で存在する。
メルカトル級数：
$1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\cdots=\displaystyle\sum_{k=1}^{\infty}\dfrac{(-1)^{k-1}}{k}=\log 2$
ルジャンドルの定理
$n!$ に含まれる素因数 $p$ の数は以下のように表される：
${\displaystyle \sum_{i=1}^{\infty}\Big\lfloor \dfrac{n}{p^i} \Big\rfloor}=\Big\lfloor \dfrac{n}{p} \Big\rfloor+\Big\lfloor \dfrac{n}{p^2} \Big\rfloor+\Big\lfloor \dfrac{n}{p^3} \Big\rfloor+\cdots$
ただし，ここで $\lfloor x \rfloor$ は $x$ を超えない最大の整数を表す。
Muirheadの不等式：
各成分が非負で非増加な数列 $a=(a_1, a_2,\cdots , a_n), b=(b_1, b_2,\cdots, b_n)$ と，任意の非負実数 $x_1, x_2, \cdots, x_n$ に対して，$[a]\succeq [b]$ ならば
$\displaystyle\sum_{sym}\prod_{i=1}^nx_i^{a_i}\geq\displaystyle\sum_{sym}\prod_{i=1}^nx_i^{b_i}\\$
等号成立条件は，$a=b$ または， $x_1=x_2=\cdots=x_n$
(i)$ A+B+C=\pi$ のとき
$\tan A+\tan B+\tan C=\tan A \tan B\tan C$
(ii) $\alpha+\beta+\gamma=\dfrac{\pi}{2}$ のとき
$\dfrac{1}{\tan \alpha}+\dfrac{1}{\tan \beta}+\dfrac{1}{\tan \gamma}=\dfrac{1}{\tan \alpha \tan \beta\tan \gamma}$
素数は無限に存在する
バーゼル問題：平方数の逆二乗和は $\dfrac{\pi^2}{6}$ に収束する。つまり，
$\displaystyle\sum_{k=1}^{\infty}\dfrac{1}{k^2}=1+\dfrac{1}{4}+\dfrac{1}{9}+\cdots=\dfrac{\pi^2}{6}$
データ群の特徴を一つの数値で表したものを代表値と呼ぶ。代表値の中でも平均値，中央値，最頻値が有名。
恒等式
$\sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}$
$\sqrt{a+b-2\sqrt{ab}}=\sqrt{b}-\sqrt{a}$
を用いて二重根号を外すことができる。
共分散 $\mathrm{Cov}(X,Y)$ は二組の対応するデータの間の関係を表す数値である。
データを $(x_1,\:y_1),(x_2,\:y_2),\cdots,(x_n,\:y_n)$ とおくとき，
$\mathrm{Cov}(X,Y)=E[(X-\mu_X)(Y-\mu_Y)]$
部分分数分解：
分母が因数分解されているような分数はいくつかの分数に分解できる。
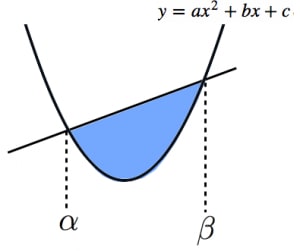
$\dfrac{1}{6}$ 公式：
放物線 $y=ax^2+bx+c$ と直線 $y=px+q$ の交点の $x$ 座標を $\alpha, \beta\:(\alpha < \beta)$ とおくとき，
放物線と直線で囲まれた部分の面積は，
$\dfrac{|a|}{6}(\beta-\alpha)^3$
リーマン予想：ゼータ関数の非自明な零点の実部は $\dfrac{1}{2}$ である。
判別式：
二次の多項式 $ax^2+bx+c$ の判別式を $D=b^2-4ac$ とする。
ユークリッドの互除法：
自然数 $a,b \:(a\geq b)$ に対して，$a$ を $b$ で割った余りを $r$ とおくとき
gcd($a$, $b$)=gcd($b$, $r$)
が成立し，これを繰り返し用いると $a$ と $b$ の最大公約数が求まる。
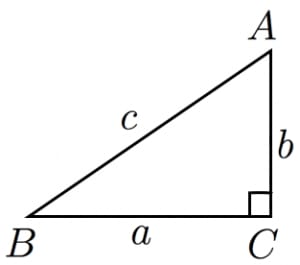
三平方の定理（ピタゴラスの定理）：$\angle C=90^{\circ}$ であるような直角三角形において，$a^2+b^2=c^2$
二進法と十進法について。二進数と十進数を互いに変換する方法と計算例，小数を含む場合についても解説します。
定理：
すべての原始ピタゴラス数は，$\begin{pmatrix}3\\4\\5\end{pmatrix}$ に対して，3つの行列 $A,B,C$ のどれかをかける操作を何度か繰り返すことで作れる。ただし，
$A=\begin{pmatrix}1&-2&2\\2&-1&2\\2&-2&3\end{pmatrix}$，
$B=\begin{pmatrix}1&2&2\\2&1&2\\2&2&3\end{pmatrix}$，$C=\begin{pmatrix}-1&2&2\\-2&1&2\\-2&2&3\end{pmatrix}$
ピタゴラス数に関する非常におもしろい定理です。この定理の主張と証明を詳しく解説します。
数列における余りの周期性について，以下の2つの話題を紹介します。
- 漸化式で表される数列における，割り算の余りの周期性（受験レベル）
- 特に，フィボナッチ数列における周期について（難しい）
この記事では，超幾何級数について紹介します。いくつか例を見ながら，超幾何級数に慣れ親しみましょう。
当サイトの管理人が，ルール（定義）と事実（定理）をきちんと区別してほしい！ というテーマで、算数の本を出版しました。
自信作です。（特に，数学があまり得意でない方に）書店にて中身を確認していただければ嬉しいです。
Popoviciu の不等式：
$f(x)$ が下に凸な関数のとき，任意の $x,y,z$ に対して(※)，
$f(x)+f(y)+f(z)+3f\left(\dfrac{x+y+z}{3}\right)\\
\geq 2\left\{f\left(\dfrac{x+y}{2}\right)+f\left(\dfrac{y+z}{2}\right)+f\left(\dfrac{z+x}{2}\right)\right\}$
※より厳密に言うと「$f$ は区間 $I\subseteq\mathbb{R}$ から $\mathbb{R}$ への関数で，$x,y,z$ は区間 $I$ に含まれる任意の実数」
この記事では，Popoviciu の不等式の意味と，2通りの証明を紹介します。
Hlawka’s Inequality：
任意の複素数 $x,\:y,\:z$ に対して，
$|x|+|y|+|z|+|x+y+z|\\
\geq |x+y|+|y+z|+|z+x|$
Hlawka’s Inequality（フラカの不等式）について紹介します。
極座標平面において，図のように $\theta=\alpha,\:\theta=\beta,\:r=r(\theta)$ で囲まれた，$x$ 軸の上側にある図形を $D$ とする。$D$ を $x$ 軸(始線)の回りに回転させてできる立体の体積は，
$\dfrac{2}{3}\pi\displaystyle\int_{\alpha}^{\beta} r(\theta)^3\sin\theta d\theta$
極座標における回転体の体積公式について，例題と証明方法などを紹介します。
周の長さが一定である図形の中で，面積が最大のものは円です。（等周定理）
等周定理の厳密な証明は少し大変なので，ここでは等周定理に関連して「対称性が高い図形は面積が大きい」というテーマで，高校数学で分かる性質をいくつか紹介します。
たすきがけによる因数分解のやり方を復習した後，たすきがけを用いない方法を解説します。
この記事では，以下のような数列について考えます。
1, 11, 21, 1211, 111221, 312211, $\dots$
面白い性質と規則性を持った数列です。