ユークリッドの互除法の証明と不定方程式

更新 2021/03/07

ユークリッドの互除法（ごじょほう）とは，大きな数たちの最大公約数を素早く計算する方法です。

この記事では，ユークリッドの互除法のやり方 や ユークリッドの互除法の不定方程式への応用方法 などを解説します。

ユークリッドの互除法の例

ユークリッドの互除法では，以下の 重要な性質 を使って最大公約数の計算を行います。

重要な性質

割り算の等式： $a=bq+r$ において，

「 $a$ と $b$ の最大公約数」＝「 $b$ と $r$ の最大公約数」

例

ユークリッドの互除法を使って $390$ と $273$ の最大公約数を計算してみましょう。

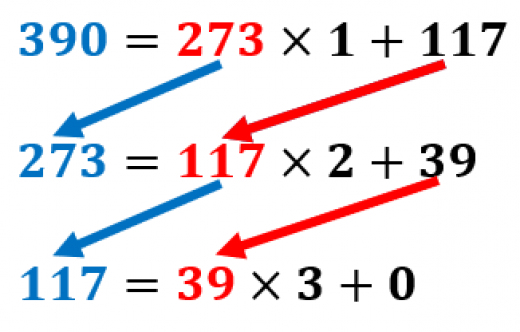
ユークリッドの互除法の例

まず， $390$ を $273$ で割ると，商が $1$ で余りが $117$ です：
$390=273\times 1+117$
よって，重要な性質 より
「 $390$ と $273$ の最大公約数」＝「 $273$ と $117$ の最大公約数」
次に， $273$ を $117$ で割ります：
$273=117\times 2+39$
よって，重要な性質 より
「 $273$ と $117$ の最大公約数」＝「 $117$ と $39$ の最大公約数」
次に， $117$ を $39$ で割ります：
$117=39\times 3+0$
割り切れました！　つまり「 $117$ と $39$ の最大公約数」は $39$ です。

以上により「 $390$ と $273$ の最大公約数」が $39$ であることが分かりました。

このように，重要な性質 を使って，繰り返し（割り切れるまで）割り算をしていき最大公約数を求める方法をユークリッドの互除法と言います。

最大公約数の記号

以下では， $a$ と $b$ の最大公約数のことを $\mathrm{gcd}(a,b)$ と表します。「最大公約数」は画数が多くて書きたくないからです。難しい記号ではありません。

ユークリッドの互除法の証明

ユークリッドの互除法で用いた，
重要な性質：
gcd(a,b)=gcd(b,r)\mathrm{gcd}(a, b)=\mathrm{gcd}(b,r)gcd(a,b)=gcd(b,r)
を証明します。
証明
aaa を bbb で割った商を qqq，余りを rrr とおくと，a=bq+r
a = bq + r
a=bq+r
となる。
gcd(b,r)≥gcd(a,b)\mathrm{gcd}(b,r) \geq \mathrm{gcd}(a,b)gcd(b,r)≥gcd(a,b)
と
gcd(a,b)≥gcd(b,r)\mathrm{gcd}(a,b) \geq \mathrm{gcd}(b,r)gcd(a,b)≥gcd(b,r)
が似たような方法で証明できる(*)ので，
gcd(a,b)=gcd(b,r)\mathrm{gcd}(a,b) = \mathrm{gcd}(b,r)gcd(a,b)=gcd(b,r)
がわかる。
(* 上側の不等式の証明)
aaa と bbb は gcd(a,b)\mathrm{gcd}(a,b)gcd(a,b) の倍数なので，r=a−bqr = a-bqr=a−bq も gcd(a,b)\mathrm{gcd}(a,b)gcd(a,b) の倍数になる。よって，gcd(a,b)\mathrm{gcd}(a,b)gcd(a,b) は bbb と rrr の公約数。最大公約数は公約数の中で最大のものなので，
gcd(b,r)≥gcd(a,b)\mathrm{gcd}(b,r) \geq \mathrm{gcd}(a,b)gcd(b,r)≥gcd(a,b)
(* 下側の不等式の証明)
bbb と rrr は gcd(b,r)\mathrm{gcd}(b,r)gcd(b,r) の倍数なので，a=bq+ra = bq + ra=bq+r も gcd(b,r)\mathrm{gcd}(b,r)gcd(b,r) の倍数になる。よって，gcd(b,r)\mathrm{gcd}(b,r)gcd(b,r) は aaa と bbb の公約数。最大公約数は公約数の中で最大のものなので，
gcd(a,b)≥gcd(b,r)\mathrm{gcd}(a,b) \geq \mathrm{gcd}(b,r)gcd(a,b)≥gcd(b,r)
割り算を繰り返し行うと，余りの定義より
b>rb > rb>r
 なので数字はどんどん小さくなっていきます。そして，最後は必ず余りが
000
 になって停止します。そのときの割った数が，求めたい最大公約数になっています。

ユークリッドの互除法がなぜ嬉しいのか

素因数分解を利用して最大公約数を求めることもできますが，大きな数字の素因数分解よりも割り算の方が圧倒的に楽（計算量が少ない）なのでユークリッドの互除法が用いられることが多いです。

例

$318691696$ と $4729749$ を素因数分解するのは相当な気合いが必要になるが，割り算なら簡単にできそう。

ただし，実際の入試問題でこんなに大きな整数はほとんど登場しないので，最大公約数を求めるだけだったら素因数分解を用いる方法で十分です。

大学入試においては，ユークリッドの互除法は最大公約数を求める問題よりも，一次不定方程式 $ax+by=1$ に関する問題で活躍します。

一次不定方程式への応用

一次不定方程式 $ax+by=1$ の整数解 $(x,y)$ を求める問題を考えます。

例

$8x+11y=1$ を満たす整数 $(x,y)$ を求める。

$11$ と $8$ にユークリッドの互除法を適用してみる。

$11=8\cdot 1+3\\ 8=3\cdot 2+2\\ 3=2\cdot 1+1$

これをさかのぼっていく（余りの部分を順々に代入していく）。

$1=3-2\cdot 1\\ =3-(8-3\cdot 2)\cdot 1\\ =3\cdot 3+8\cdot(-1)\\ =(11-8\cdot 1)\cdot 3-8\\ =8\cdot (-4)+11\cdot 3$

これは $8x+11y=1$ の形になっている

つまり， $(-4,3)$ が解の1つ。

よって，一次不定方程式ax+by=cの整数解にあるように，解が1つ見つかれば一般解が構成できる：

一般解は $(-4+11n,3-8n)\:$ ( $n$ は整数)

ポイントは，ユークリッドの互除法の式を用いて， $1$ を $2x+3y$ の形で表す→ $3x+8y$ の形で表す→ $8x+11y$ の形で表す，と変形していくことです。慣れれば機械的に計算できます。

まとめ

ユークリッドの互除法

自然数 $a,b \:(a\geq b)$ に対して， $a$ を $b$ で割った余りを $r$ とおくとき

$\mathrm{gcd}(a, b)=\mathrm{gcd}(b,r)$

が成立し，これを繰り返し用いると $a$ と $b$ の最大公約数が求まる。

gcdは最大(greatest) 公(common) 約数(divisor)　の略

Tag:不定方程式の解き方まとめ

Tag:数学Aの教科書に載っている公式の解説一覧

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！