Popoviciu の不等式
更新
が下に凸な関数のとき,任意の に対して(※),
※より厳密に言うと「 は区間 から への関数で, は区間 に含まれる任意の実数」です。
この記事では,Popoviciu の不等式の意味と,2通りの証明を紹介します。
Popoviciu の不等式について
Popoviciu の不等式について
凸関数とは,グラフ上の二点を結んだ線分が常にグラフの上側にあるような関数のことです。→上に凸,下に凸な関数と二階微分
凸関数に関する不等式といえば,イェンゼンの不等式が有名です。→イェンゼンの不等式の3通りの証明
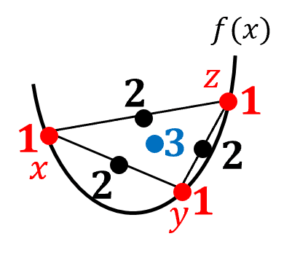
Popoviciu の不等式は,少し長くて一見覚えにくいですが,図のように三角形を書くと理解しやすいです。赤が三角形の頂点,黒が中点,青が重心です。 「頂点+3×重心」が「2×中点」よりも強いという,なかなか美しい不等式です。
Popoviciu の不等式の証明1
Popoviciu の不等式の証明1
Popoviciu の不等式を証明します。イェンゼンの不等式を3つ組み合わせればできそうな気がします。しかし「対称な不等式を3つ組み合わせる」という方針ではなかなかうまくいかず,ひと工夫必要です。
対称性より, の場合のみ証明すれば十分。さらに, の場合を証明する(つまり, が に近い場合を証明する。 に近い場合も同様に証明できるし,対称性より明らかとも言える)
まず,イェンゼンの不等式より,
なので,Popoviciu の不等式の「残りの4項分」:
を証明すれば十分。

は と重心の間にあるので,ある が存在して,
よって,イェンゼンの不等式より 同様に,ある が存在して,
から, 赤色の不等式2つを足し上げれば「残りの4項分」が証明できそう!
( であることがわかれば,2つの式を足し上げることで「残りの4項分」が証明できる)
実際, を定義した2つの式を加えると,
となるが,これを について解くと, になる( が消える!)
Popoviciu の不等式の証明2
Popoviciu の不等式の証明2
Karamataの不等式を使って証明することもできます。Karamataの不等式をきちんと理解していれば,一瞬で証明できます。
さきほどの証明と同様に, かつ の場合を証明する。
の方が よりも「偏っている」ことを確認すればよい。それぞれ大きい順に並べると,
および となるが, であることは簡単に確認できる。
ちなみに,Popoviciu の不等式は,Hlawka’s Inequalityの一般化になっています。
「Popoviciu」という名前が印象的なので,記憶に残りやすい不等式です。











