極座標における回転体の体積公式

極座標平面において,図のように で囲まれた, 軸の上側にある図形を とする。 を 軸(始線)の回りに回転させてできる立体の体積は,
極座標における回転体の体積公式について,例題と証明方法などを紹介します。
回転体の体積公式と球の体積公式の関係
回転体の体積公式と球の体積公式の関係
まず,具体例として の場合を考えてみます。極座標における回転体の体積公式を使ってみると,回転体の体積は,
となります。
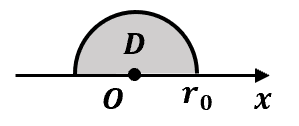
一方, は半径 の円の上側半分を表すので,球の体積公式を使うことでも,体積が であることが分かります。
つまり,極座標における回転体の体積公式 は,球の体積公式 を拡張したもの,とみなせます。
体積公式を使う例題
体積公式を使う例題
極座標における回転体の体積公式を使って,2009年京都大学理系第5問の一般化を解いてみます(京大の問題は )。
極方程式 で表される図形で囲まれる部分 を 軸の回りに回転させてできる立体の体積 を計算せよ。ただし, とする。

極座標における回転体の体積公式を使って計算してみます。 は 軸に関して対称であることに注意すると,
例題の補足
例題の補足
-
極方程式 で表される図形のことを,リマソンと言います。リマソン(英語版Wikipedia)
-
特に, の場合をカージオイドと言います(カージオイド曲線のグラフ,面積,長さ)。カージオイドは有名ですが,リマソンはわりとマニアックだと思います。私自身,大学受験時にはリマソンという名前や体積公式は知りませんでした。
-
「愚直な方法」と「極座標における回転体の体積公式を使った方法」の両方で計算することで。検算できます。
体積公式の証明
体積公式の証明
パップスギュルダンの定理を使って公式を証明します。
また,極座標の面積公式の証明を理解しているとスムーズです。
から の間の微小部分 を 軸の回りに回転させた立体の体積 をパップスギュルダンの定理を使って計算する。
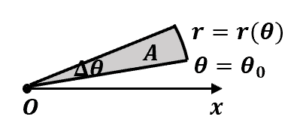
が十分小さいとき, を三角形とみなすと,
の面積
の重心の 座標
よって,微小部分の体積は,
これを積分することで,回転体の体積公式を得る。
注:冒頭の主張では「 軸の上側にある図形」と限定しています。 軸の下側にある場合は となりますが,そのような場合でも と絶対値をつけるとこの式は成立します。
紹介した証明方法と例題は,高校時代の恩師のy先生に最近教えていただいたものです!










