分野: 積分

$\displaystyle\int (x-a)^tdx=\dfrac{1}{t+1}(x-a)^{t+1}+C \hspace{10mm} (t\neq -1)$

シュワルツの不等式の積分バージョン：
$\displaystyle\left(\int_p^q f(x)^2dx\right)\left(\int_p^q g(x)^2dx\right)\\
\geq\displaystyle\left(\int_p^q f(x)g(x)dx\right)^2$

等号成立条件は $g(x)=tf(x)$ となる $t$ が存在する（または $f=0$）こと。

$\displaystyle\int e^{ax}\cos bxdx=\dfrac{e^{ax}}{a^2+b^2}(a\cos bx+b \sin bx)+C$
$\displaystyle\int e^{ax}\sin bxdx=\dfrac{e^{ax}}{a^2+b^2}(a\sin bx-b \cos bx)+C$

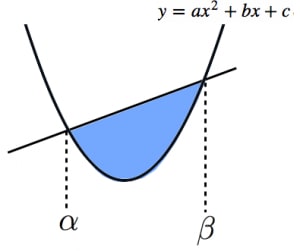
$\dfrac{1}{6}$ 公式：
放物線 $y=ax^2+bx+c$ と直線 $y=px+q$ の交点の $x$ 座標を $\alpha, \beta\:(\alpha < \beta)$ とおくとき，
放物線と直線で囲まれた部分の面積は，
$\dfrac{|a|}{6}(\beta-\alpha)^3$

$m, n$ が $0$ 以上の整数のとき，以下のような積分公式が成立する（ベータ関数の積分公式）：

(i)　第一種オイラー積分
$\displaystyle\int_{\alpha}^{\beta} (x-\alpha)^m(\beta-x)^ndx=\dfrac{m!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$

(ii) 特に，$\alpha=0, \beta=1$ とすると，
$\displaystyle\int_0^1 x^m(1-x)^ndx=\dfrac{m!n!}{(m+n+1)!}$

$\displaystyle\int \dfrac{1}{\sin x}dx=\dfrac{1}{2}\log\left(\dfrac{1-\cos x}{1+\cos x}\right)+C$
$\displaystyle\int \dfrac{1}{\cos x}dx=\dfrac{1}{2}\log\left(\dfrac{1+\sin x}{1-\sin x}\right)+C$

$\sin^n x, \cos^n x$ の定積分は部分積分と漸化式を使って求めることができる。

公式1：$\displaystyle\int \dfrac{dx}{\sqrt{x^2+a^2}}=\log(x+\sqrt{x^2+a^2})$
公式2：$\displaystyle\int \sqrt{x^2+a^2}dx=\dfrac{1}{2}(x\sqrt{x^2+a^2}+a^2\log(x+\sqrt{x^2+a^2}))$

ヤングの不等式：
$a, b > 0,p,q > 1, \dfrac{1}{p}+\dfrac{1}{q}=1$ を満たすとき，
$\dfrac{a^p}{p}+\dfrac{b^q}{q}\geq ab$

$A=B$ のとき，$A=\dfrac{A+B}{2}$
という自明な等式を用いて定積分を計算できる場合がある

ガウス積分とは，以下のような定積分のことです。
$\displaystyle\int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\dfrac{\pi}{a}}$
（ただし $a > 0$）

面積は微分の逆の操作を用いて求めることができる。

三角関数の積の積分は積和公式で和に直すことで積分できる。

$r(\theta)$ が連続関数のとき，極方程式 $r=r(\theta)$ で表される曲線と $\theta=\alpha, \beta$ で囲まれる部分の面積は，
$\displaystyle\int_{\alpha}^{\beta}\dfrac{1}{2}r(\theta)^2d\theta$

バウムクーヘン分割：
連続関数 $y=f(x)$，$x$ 軸，$x=\alpha,x=\beta\:$(ただし $0\leq \alpha <\beta$)で囲まれた図形を $y$ 軸の回りに回転させてできる立体の体積 $V$ は，
$V=\displaystyle\int_{\alpha}^{\beta}2\pi x|f(x)|dx$

パップスギュルダンの定理：
面積が $S$ である平面図形 $A$ がある。 $A$ を直線 $l$ の回りに回転させてできる回転体の体積 $V$ は， $V=2\pi g_xS=$(重心の移動距離) $\times S$
（$g_x$ は重心と回転軸の距離）
ただし，$A$ を回転させる過程で $A$ 自身とは重ならないとする。

傘型分割：
$y\leq mx,\:y\geq f(x),\\\:a\leq x\leq b$
が定める図形を $l:y=mx$ の回りに回転させてできる図形の体積 $V$ は，
$V=\pi\cos\theta\displaystyle\int_a^b(mx-f(x))^2dx$
ただし，$\theta$ は $l$ と $x$ 軸のなす角で，$\tan\theta=m$

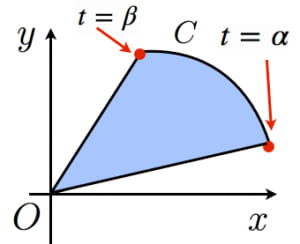
ガウスグリーンの定理：
$x=x(t),\:y=y(t)$ と媒介変数表示された曲線 $C$ がある。 $\alpha\leq t\leq \beta$ の範囲で $t$ の増加とともに $(x(t),y(t))$ が原点中心に反時計回りに動くとき，動径が掃いた部分の面積は， $S=\displaystyle\int_{\alpha}^{\beta}\dfrac{1}{2}(xy’-yx’)dt$

弧長積分1：$f$，$g$ が連続かつ微分可能で $f’$，$g’$も連続とする。
$x=f(t), y=g(t)$ と媒介変数表示された曲線 $C$ の $\alpha\leq t\leq \beta$ の部分の長さは， $\displaystyle\int_{\alpha}^{\beta}\sqrt{f'(t)^2+g'(t)^2}dt$

弧長積分2：$f$ は連続かつ微分可能で $f’$も連続とする。
$y=f(x)$ で表される曲線 $C$ の $a\leq x\leq b$ の部分の長さは， $\displaystyle\int_{a}^{b}\sqrt{1+f'(x)^2}dx$

$n$ 次元単位超球の体積は， $V_n=\dfrac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}$

台形公式を使うことで定積分の値を近似的に求めることができる。

置換積分を行うときには変数を置き換えるだけでなく，微分をかけるのを忘れないように。定積分の場合は積分区間の変更も必要。

対数関数の不定積分： $\displaystyle\int \log xdx=x\log x-x+C$

$\displaystyle\int \tan xdx=-\log |\cos x|+C$
$\displaystyle\int \tan^2 xdx=\tan x-x+C$
$\displaystyle\int \tan^n xdx=\dfrac{1}{n-1}\tan^{n-1}x-\int\tan^{n-2}xdx$

三角関数の有理式の積分は $\tan\dfrac{x}{2}=t$ と置換することによって必ず計算できる。

$\displaystyle\int e^xdx=e^x+C$
$\displaystyle\int a^xdx=\dfrac{a^x}{\log a}+C\:(a > 0)$

定積分で表された関数の微分の公式：
$\displaystyle\frac{d}{dx}\int_a^xf(t)dt=f(x)$
（ただし，$f(t)$ は $t$ に関する1変数の関数）

$0$ 以上の整数 $n$ と，$\displaystyle\sum_{k=1}^n|a_k|\leq 1$ を満たす実数 $a_1,\cdots, a_n$ に対して，
$\displaystyle\int_0^{\infty}\dfrac{\sin x}{x}\left(\prod_{k=1}^n\dfrac{\sin a_kx}{a_kx}\right)dx=\dfrac{\pi}{2}$

微分すると $f(x)$ になるような関数 $F(x)$ を $f(x)$ の原始関数と言う。

Sophomore’s dream:
(1) $\displaystyle\int_{0}^1\dfrac{1}{x^x}dx=\sum_{n=1}^{\infty}\dfrac{1}{n^n}$
(2) $\displaystyle\int_{0}^1x^xdx=-\sum_{n=1}^{\infty}(-n)^{-n}$

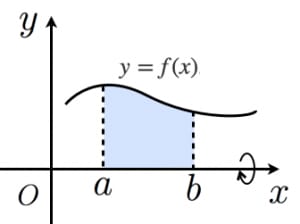
$y=f(x)$，$x=a$，$x=b$，$x$ 軸で囲まれた領域を $x$ 軸のまわりに回転させてできる図形の体積は，
$V=\displaystyle\int_{a}^b\pi \{f(x)\}^2dx$

$1$ と $\sqrt{2}$ の算術幾何平均 $M(1,\sqrt{2})$ は，単位円周の長さ $l=2\pi$ とレムニスケートの長さ $L$ の比に等しい：
$M(1,\sqrt{2})=\dfrac{l}{L}$

$\displaystyle\int_0^{\infty}\dfrac{x^3}{e^x-1}dx=\dfrac{\pi^4}{15}$

極座標平面において，図のように $\theta=\alpha,\:\theta=\beta,\:r=r(\theta)$ で囲まれた，$x$ 軸の上側にある図形を $D$ とする。$D$ を $x$ 軸(始線)の回りに回転させてできる立体の体積は，
$\dfrac{2}{3}\pi\displaystyle\int_{\alpha}^{\beta} r(\theta)^3\sin\theta d\theta$