ガウス積分の公式の2通りの証明
ガウス積分はとても有名な定積分の公式です。正規分布の計算などで活躍します。
ガウス積分とは,以下のような定積分のことです。
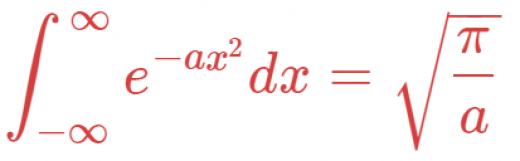
ただし,この記事では とします。
ガウス積分の公式一覧・応用を述べたあと,ガウス積分の証明を2通り紹介します。
ガウス積分にまつわる公式
ガウス積分にまつわる公式
まずは,ガウス積分に関連する公式の一覧です。
-
不定積分 は初等関数で表せませんが, や の定積分は計算できるというのがおもしろいです。
-
の場合のみ書きましたが, でも計算できます。
-
ガウス積分を手っ取り早く計算・検算したい人は,wolframalpha がおすすめです。例えば \int_{-\infty}^{\infty}x^2e^{-3x^2+4x+5}dx と入力すると を計算できます。
ガウス積分の応用
ガウス積分の応用
-
ガウス積分の応用の代表例は,正規分布(ガウス分布)についてのいろいろな計算です。ガウス積分について知っていれば,ガウス分布の確率密度関数:
の理解が深まります。→正規分布の基礎的なこと -
ガウス分布の分散の計算に公式3が活躍します。
-
レイリー分布 の期待値の計算にもガウス積分が活躍します。
ガウス積分の証明
ガウス積分の証明
-
公式1: の証明が少し大変です。
-
公式1さえ証明できれば公式2~公式11の証明は簡単です(後述します)。
-
公式1の証明を2通り紹介します。ガンマ関数を用いる方法と,重積分を用いる方法です。
ガンマ関数を用いる証明
ガウス積分は,ほぼ高校数学の範囲内で証明できます。
ただし(高校生でも頑張れば理解できるが少し難しい)前提知識として「ガンマ関数とベータ関数の関係」を使います。
参考:ベータ関数の積分公式の下の方を参照してください。
階乗の一般化であるガンマ関数 を利用します。ガンマ関数は直接計算できないので,ベータ関数に変換してから置換積分で計算します。
ガンマ関数の定義より
であり, と置換すると,
一方,ガンマ関数とベータ関数の関係より,
ここで と置換すると,
より,
以上より,
※積分区間が有限でないのでガウス積分は広義積分です。そのため,厳密には高校数学範囲外です。
重積分を用いる証明
次は重積分を用いる方法です。表記は少しゴツイですが,内容は単純です。
を出現させるために極座標を用います。極座標が使える形にするために最初にあえて二乗します。
ガウス積分の値を とおく。
ここで と置換すると,ヤコビアンは なので,
よって,
補足:
-
最初の部分で とできることを用いました。(フビニの定理)これは,シグマの二重和が分解できることの一般形です。シグマ計算を機械的に行うための3つの公式の最後の部分。
-
重積分の変数変換,ヤコビアンに関しては厳密には大学内容が必要です。→ヤコビ行列,ヤコビアンの定義と極座標の例
-
平面上において から の間にある部分の面積が と近似できることと関係しています。全平面上で積分する際に を固定して で積分し,最後に で積分します。

残りの公式の証明
残りの公式の証明
公式1: さえ証明できれば公式2~公式11の証明は簡単です。

奇関数の積分なので,
※偶関数と奇関数の積分の性質については,→偶関数と奇関数の意味,性質などまとめ
部分積分を使うと,
よって,
- として公式1を使うと公式3を得る:
- さらに として公式3を使うと公式5を得る:
公式6の証明は少し特殊です。指数の中身の二次関数を平方完成します。
ここで, と置換して公式1を使うと,上式は
となる。
偶関数の性質と公式1より,
同様に公式3から公式9が導ける。公式5から公式11が導ける。
普通に原始関数が求まるパターンです:
公式3の証明と同様に,部分積分すると以下を導ける: として公式8を使うと公式10を得る。
置換積分のオンパレードでしたね。ちなみに,多変数のガウス積分の公式もあります: →多変数のガウス積分
Tag:正規分布の基礎的な知識まとめ











