ガウスグリーンの定理の入試への応用
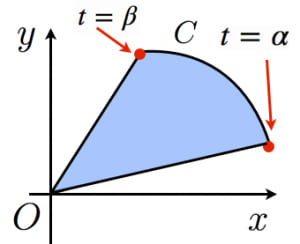
と媒介変数表示された曲線 がある。 の範囲で の増加とともに が原点中心に反時計回りに動くとき,動径が掃いた部分の面積は,
ガウスグリーンの定理の例題
ガウスグリーンの定理の例題
とりあえず簡単な例でガウスグリーンの定理の威力を実感してみてください。入試でも頻出の曲線「アステロイド」です。
で表される曲線で囲まれる面積 を求めよ。
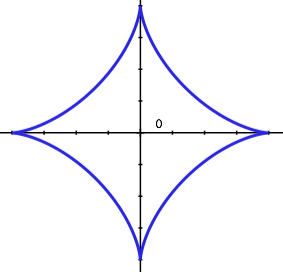
より,
よって,ガウスグリーンの定理より,
これはアステロイド曲線の重要な性質まとめで解説した正攻法による積分計算よりも圧倒的に楽です!
→高校数学の問題集 ~最短で得点力を上げるために~のT135では,この積分についてさらに詳しい解説と計算ミスを減らすコツを解説しています。
ガウスグリーンの定理について
ガウスグリーンの定理について
- 媒介変数表示されている& の増加とともに反時計回りに動く(偏角が増加する)という二つの条件を満たしているときは非常に有効な公式です。通常の方法で積分するよりも大幅に計算量を減らせることが多いです。
- 媒介変数表示ではなく極方程式で表されている場合は極方程式の面積公式と例題で紹介した公式を使いましょう。
- ガウスグリーンの定理はベクトル解析の定理で,本当はもっと一般的な形をしています。冒頭で述べた式は高校数学の求積で使えるように特殊化したものです。
- 検算テクニックとして役立ちます。
ガウスグリーンの定理の証明
ガウスグリーンの定理の証明
他の面積公式と同様,厳密な証明にははさみうちの原理が必要で難しいので以下の「簡単な説明」を理解しておけば十分です。
面積を求める図形を原点を中心とする微小な三角形を寄せ集めたものとみなします。原点を頂点の一つとする三角形の面積はサラスの公式で紹介した公式(i)で一発です。
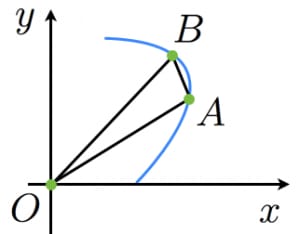
媒介変数が から まで動くときに動径が掃く面積を微小な三角形で近似する。原点 および , がなす三角形の面積は,有名な面積公式から
ここで, が少し増加すると点は反時計回りに動くという仮定から絶対値の中身は正なので(→注)
両辺を で割って の極限を取ると,
これを から まで積分すればガウスグリーンの公式を得る。
注: がともに第一象限にあるとき,傾きの関係から の分母を払うとOK。他の場合も同様(きちんと書くと場合分けが煩雑)。
ちなみに,これは外積 の 成分が正であることを示しています(右ねじの法則)。
最近きれいな曲線をパソコンで描く技術を身につけました!











