検算テクニック

シンプソンの公式の証明と例題

レベル: ★最難関大学    

シンプソンの公式：
$f(x)$ が三次以下の関数のとき，
$\displaystyle\int_a^bf(x)dx=\dfrac{(b-a)}{6}\{f(a)+4f(\dfrac{a+b}{2})+f(b)\}$

三次関数の定積分を素早く計算（検算）することができます！

ロピタルの定理の条件と例題

レベル: ★入試対策    

ロピタルの定理（大雑把バージョン）：
$\displaystyle\lim_{x\to a}\dfrac{f(x)}{g(x)}$ が $\dfrac{0}{0}$ または $\dfrac{\infty}{\infty}$ の不定形で「ある条件」を満たせば，
$\displaystyle\lim_{x\to a}\dfrac{f(x)}{g(x)}=\lim_{x\to a}\dfrac{f'(x)}{g'(x)}$

位相が等差数列である三角関数の和の公式

レベル: ★最難関大学    

（位相が等差数列なら）複素指数関数と等比数列の和の公式を用いて三角関数の和を計算することができる：
$\displaystyle\sum_{k=0}^n\sin(\theta+k\phi)=\dfrac{\sin(\frac{(n+1)\phi}{2})\sin(\theta+\frac{n\phi}{2})}{\sin\frac{\phi}{2}}$
$\displaystyle\sum_{k=0}^n\cos(\theta+k\phi)=\dfrac{\sin(\frac{(n+1)\phi}{2})\cos(\theta+\frac{n\phi}{2})}{\sin\frac{\phi}{2}}$

三角関数の和を求めるタイプの問題に対するかなり万能な方法です。

分数関数の極値を求める２つのテクニック

レベル: ★入試対策    

分数関数の極値を求めるテクニックを2つ紹介します。

1つ目は $y=\dfrac{f(x)}{g(x)}$ の形の関数ならどんなものでも使える実践的なテクニック，
2つ目は分母が2次式，分子が1次式の場合にのみ使えるエレガントなテクニックです。

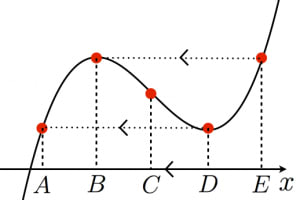
三次関数の対称性と４等分の法則

レベル: ★入試対策    
三次関数の対称性

三次関数のグラフに関して以下の性質が成り立つ
対称性1：（変曲点に関して）点対称である
対称性2：図において，$A,B,C,D,E$ は等間隔に並んでいる（4等分の法則）

攪乱順列の公式

レベル: ★最難関大学    

$1, 2,\cdots, n$ を並び替えてできる順列のうち，全ての $i=1, 2, \cdots, n$ に対して $i$ 番目が $i$ でないものの個数 $a_n$ は，以下の式で表される：
$a_n=n!\displaystyle\sum_{k=2}^n\dfrac{(-1)^k}{k!}$

三角関数と指数関数の積の積分

レベル: ★入試対策    

三角関数と指数関数の積の積分は部分積分を2回行って求めるのが定石ですが，計算量も多くミスしやすいので，公式として覚えておくとスピードアップや検算に役立ちます：

$\displaystyle\int e^{ax}\cos bxdx=\dfrac{e^{ax}}{a^2+b^2}(a\cos bx+b \sin bx)+C$
$\displaystyle\int e^{ax}\sin bxdx=\dfrac{e^{ax}}{a^2+b^2}(a\sin bx-b \cos bx)+C$

トレミーの定理とその証明，応用例

レベル: ★最難関大学    

トレミーの定理：円に内接する四角形 $ABCD$ において, $AB×CD＋AD×BC＝AC×BD$

トレミーの定理

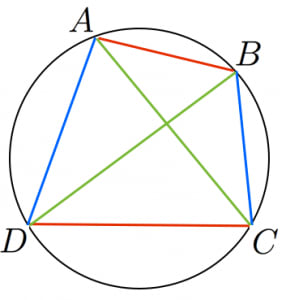
非常に美しい定理で応用も広いです。
大学入試問題では，検算に用いる場合が多いです。

この記事ではトレミーの定理の2通りの証明と，トレミーの定理の応用例を3つ紹介します。まずは応用例から！