漸化式の解き方12パターンと応用例まとめ
漸化式(ぜんかしき)についてわかりやすく解説します。漸化式の意味から,解き方12パターンをすべて紹介します。
漸化式とは
漸化式とは
-
のように,数がたくさん並んでいるものを考えます。数列と呼びます。
-
数列の 番目の数を と書きます。上の例だと です。
-
漸化式とは,数列において「前の数」から「新しい数」を作る規則のことです。
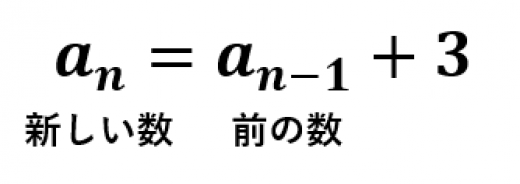
は漸化式である。この漸化式は,「 番目の数」は「 番目の数」に を加えたものという意味の式。
例えば
という条件のもとで漸化式を適用すると,
のように,数列の各項を計算できます。
漸化式の解き方1:等差数列型
漸化式の解き方1:等差数列型
, という漸化式で表される数列の一般項を計算せよ。
この漸化式は,さきほど見たように,「 番目の数」は「 番目の数」に を加えたものという意味です。つまりこの数列は,初項が で,公差が である等差数列です。よって 番目の数は,
となります。
ポイント:
このように,
というタイプの漸化式は,等差数列を理解していれば解くことができます。
漸化式の解き方2:等比数列型
漸化式の解き方2:等比数列型
, という漸化式で表される数列の一般項を計算せよ。
この漸化式は,「 番目の数」は「 番目の数」を 倍したものという意味です。つまりこの数列は,初項が で,公比が である等比数列です。よって 番目の数は,
となります。
ポイント:
このように,
というタイプの漸化式は,等比数列を理解していれば解くことができます。
漸化式の解き方3:階差数列型
漸化式の解き方3:階差数列型
, という漸化式で表される数列の一般項を計算せよ。
漸化式を繰り返し使ってみると,
となります。ここで,1からnまでの和の公式を使うと,
となるので,結局
となります。
ポイント:
このように,
というタイプの漸化式は, の和を計算することで解けます。
漸化式の解き方4:一次の二項間漸化式
漸化式の解き方4:一次の二項間漸化式
, という漸化式で表される数列の一般項を計算せよ。
漸化式は, と変形できます(※)
よって, は公比が の等比数列です。そして,初項は です。よって,
よって,
※なぜその変形が思いつくのか?
→特性方程式
の解が
だからです。詳しくはf(n)を含む二項間漸化式の2通りの解き方
の最初の例題を参照。
ポイント:
このように, というタイプの漸化式は,平行移動して等比数列にすることで解けます。
漸化式の解き方5:一次の三項間漸化式
漸化式の解き方5:一次の三項間漸化式
,, という漸化式を解け。
答えは, になります。
という三項間漸化式の解き方は3通りあります。詳細は,三項間漸化式の3通りの解き方
また,三項間漸化式が解ければ,有名なフィボナッチ数列の一般項を計算することもできます。→フィボナッチ数列の7つの性質(一般項・黄金比・互いに素)
また,一般に一次の 項間漸化式については,漸化式の特性方程式の意味とうまくいく理由 で解説しています。
漸化式の解き方6:累乗を含む二項間漸化式
漸化式の解き方6:累乗を含む二項間漸化式
, という漸化式を解け。
累乗が入った漸化式の解き方は, をかけたり割ったりすることで,より単純な漸化式に帰着できる場合が多いです。例えば,両辺を などで割って とおくことで, に関する漸化式が得られます。
与式の両辺を で割ると となる。ここで とおくと, となる。また となる。解き方4により,これを解くと が得られる。
こうして となる。
この後登場する階乗を含む漸化式と似た変形です。
難しい漸化式の解き方
難しい漸化式の解き方
上記の6パターンが解ければ漸化式の基礎はバッチリです。
ここからは,より難しい漸化式を一気に紹介します。それぞれ説明が長くなるので,詳細はリンク先の記事で詳しく説明しています。
,
このような, 型の漸化式は,階差数列を何度も取ることで解けます。
,
一次分数型の漸化式は,必要なら平行移動した上で逆数を取ることで解けます。 一次分数型の漸化式の解法と例題
, のもとで,連立漸化式
を解け。
連立漸化式は,3通りの解き方があります。例えば, を消去すると,三項間漸化式に帰着できます。 連立漸化式の3通りの解き方
,
これは6で登場した累乗を含む漸化式と解き方は近いです。
階乗を含む置き換えを使うことで,漸化式が解ける場合があります。 階乗を用いる漸化式の解法
一見解けませんが三角関数を用いることで一般項が表せる,有名な漸化式です。ロジスティック写像と漸化式
カタラン数と呼ばれる有名な数字を表す漸化式です。 カタラン数の意味と漸化式,数列の母関数とその応用例
ちなみに,解けない漸化式もたくさん存在します。つまり,上の11個の例題のように「漸化式で表される数列の一般項が のきれいな式で表せる」のはむしろ特別な場合と言えます。
漸化式の応用
漸化式の応用
-
破産の確率と漸化式
漸化式は場合の数,確率の問題でも頻繁に顔を出します。 -
sinのn乗,cosのn乗の積分公式
乗の積分といえば部分積分&漸化式。積分にも漸化式が登場。 -
漸化式で表される数列の極限
漸化式は極限にも登場します。一般項が求まらなくても数列の極限なら求まる場合もあります。 -
漸化式を用いた関数方程式の解法
関数方程式にまで漸化式が登場。
漸化式は数学のいろいろな分野に顔を出す重要な道具です。










