降べきの順と昇べきの順について
降べきの順とは,次数が下がって行くような式の表し方。
降べきの順で表した例:
昇べきの順とは,次数が上がって行くような式の表し方。
昇べきの順で表した例:
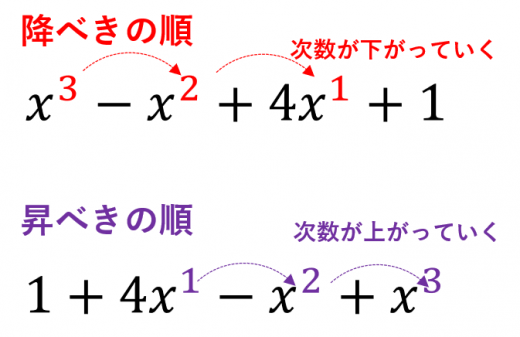
この記事では, 降べきの順と昇べきの順の意味 や, どちらを使うべきなのか などについて解説します。
降べきの順とは
降べきの順とは
多項式を,次数が高いものから順に並べることを「降べきの順に整理する」と言います。「降べき」の読み方は「こうべき」で漢字は「降冪」です。
を降べきの順に整理すると,
となる。
「べき」とは指数のことです。 降べき とは, べき(指数) がだんだん 降 りていくように整理することです。
昇べきの順とは
昇べきの順とは
逆に,次数が低い順に並べることを「昇べきの順に整理する」と言います。「昇べき」の読み方は「しょうべき」で漢字は「昇冪」です。
を昇べきの順に整理すると,
となる。
変数が複数ある場合
変数が複数ある場合
変数がいくつもある多項式については,特定の変数の次数に注目して整理することになります。 注目する変数以外は全て定数とみなします。
- について降べきの順に整理:
- について昇べきの順に整理:
- について降べきの順に整理:
- について昇べきの順に整理:
このように,多項式1つに対してもいろいろな整理の方法があります。以下では,どのように整理するのが最善なのか考えてみます。
降べきの順 VS 昇べきの順
降べきの順 VS 昇べきの順
降べきの順と昇べきの順のどちらで表すのが良いのかを考えてみます。
基本方針は 「重要なものを先頭に持ってくる」です。次数の高いものが重要なのか,定数項が重要なのか,場面に応じて使い分けます。
- 基本的には降べきの順に整理すればよいです。多くの場面では高次の項が重要だからです。
- まれに昇べきの順に整理する場面(定数項が重要な場合)が出てきます。例えば,マクローリン展開など,いろいろな関数を多項式で近似する場合は定数項が重要なのです。
- 実は,対称式の場合は降べきの順でも昇べきの順でもない整理の仕方が一番美しい場合があります。
はこのままで美しい。
例えば について降べきの順に整理すると,,
について昇べきの順に整理すると, となりいずれも汚くなってしまう。
- このように場面に応じて使い分けることが重要です。場面に相応しくない整理の仕方だと,答えは合っていても採点者に「この人はセンスがないなあ」と思われてしまいます。
そもそもなぜ式を整理するのか
そもそもなぜ式を整理するのか
「降べきの順や昇べきの順にする」というのは「式の整理」の方法の1つです。一般に,式を整理すると,
- 単純に見やすい,そのため次なる一手につなげやすい
- 因数分解しやすくなる
などの恩恵があります。どのように整理すると最大限恩恵が得られるのかを考えて,場面に応じて整理の方法を使い分けましょう。
答えが正しいだけでなく,センスのある美しい解答を書けるようになりましょう。きっと間接的に得点アップにつながります。











