グラフの平行移動(具体例と公式の証明)
関数 のグラフを 軸方向に , 軸方向に 平行移動したグラフを表す式は
つまり, を に変えて, を に変えればよい。
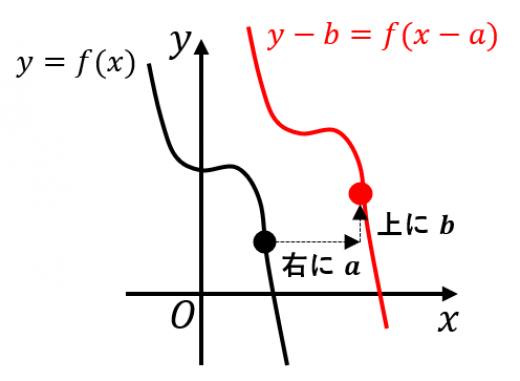
グラフの平行移動の公式について,具体例・公式の証明など解説します。
グラフの平行移動の例題
グラフの平行移動の例題
まずは,グラフの平行移動に関する例題です。
のグラフを, 軸方向に 平行移動した関数を求めよ。
を に変えればよいので,
右辺を展開すると,
のグラフを, 軸方向に , 軸方向に 平行移動した関数を求めよ。
を ,つまり に変えて を に変えればよいので,
が答え。展開して整理すると,
グラフの平行移動の公式の証明
グラフの平行移動の公式の証明
「グラフの平行移動の公式」を証明します。なぜ ではなく (マイナス符号がつく)となるのか,理由もきちんと理解しましょう。
のグラフを 軸方向に , 軸方向に 平行移動させたグラフは

-
上にある点 を平行移動して になったとする。「平行移動」の定義より,
-
上式を について解く:
(ここでマイナスが登場!) -
は 上にあるので, である。これに紫の式を代入すると,
となり, と の間に成り立つ関係式が求まった。
証明の補足
上記の証明は,以下の「方針」に基づいています。この「方針」は,より難しい変換(拡大縮小・対称移動,回転など)の場合にも使える非常に重要な考え方なので覚えておきましょう。
-
上の点 を「変換」した点を とおき, をそれぞれ で表す。
-
について解く。
-
に代入して の関係式を求める。
グラフの平行移動の様々な具体例
グラフの平行移動の様々な具体例
「平行移動」という言葉が明示的に使われていないものも含まれています。平行移動の構造を見つけたらこの公式を思い出しましょう。
一次関数の平行移動
傾きが で を通る直線の方程式は(原点を通る傾き の直線を平行移動させたものなので),
となります。
二次関数の平行移動
を平行移動させたグラフで頂点が となるものは,
となります。 軸方向に , 軸方向に 平行移動です。
円の平行移動
中心 ,半径 の円の方程式は,
となります。 軸方向に , 軸方向に 平行移動です。
その他の関数
分数関数,無理関数,楕円,双曲線などのグラフを描くときも, 「原点を中心にした基本的なものを平行移動させる」と考えればスッキリすることが多いです。
平行移動と拡大を合わせるとかなり多くのグラフを同一視できます。











