フォードの円
更新
中心が で直径が である円を並べると美しい。
フォードの円と呼ばれる美しい円たちについて紹介します。
フォードの円とは
フォードの円とは
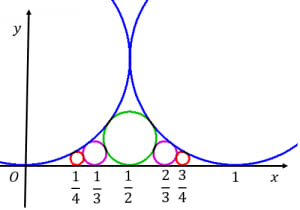
まず,値が 以上 以下で,分母が 以下の既約分数を並べます。例えば のとき,
という感じです(左端は ,右端は とします)。
ちなみに,この数列はファレイ数列と呼ばれます。
次に,各分数 に対して,中心が で直径が である円を書きます。各円は 軸に接することに注意してください。
このとき, 隣り合う分数に対応する円は互いに接します!この円(たち)のことをフォードの円と言います。
のときは冒頭の図のような感じです。
接することの証明
接することの証明
ファレイ数列の性質を使います。→ファレイ数列の4つの性質とその証明
隣り合う既約分数 と に対応する円が接することを証明する。
それぞれの円の中心間の距離を とおくと,
一方,2つの円の半径を とおくと,
この2つが等しいことを証明すればよい。差を計算すると,
ここで,ファレイ数列の性質3より, なので,上式は になる。
フォードの円の面積の総和
フォードの円の面積の総和
分母の上限 をどんどん大きくしていったときのフォードの円の面積の総和を計算してみましょう(ただし,便宜上 に対応する円は除きます)。
まず,分母が である既約分数は, 個あります。→オイラーのファイ関数のイメージと性質
よって,それらの分数に対応する円の面積の和は,
したがって,全てのフォードの円の面積の和は,
となります。
実は,上式はゼータ関数を用いて
と書けることが知られています。
参考文献:Introduction to Analytic Number Theory
具体的な値は くらいです。
※1998年東大理系前期第3問が,フォードの円に関連する問題のようです!(読者の方に教えていただきました)
ゼータ関数で書けることの証明はきちんと理解していません(大雑把に証明を読んだ程度)が,美しいです!











