歪度,尖度の定義と意味
確率変数 が従う分布の尖度,歪度を以下のように定義する:
歪度:
尖度:
統計学における歪度・尖度の定義と意味を解説します。
この記事では確率分布の平均を ,標準偏差を (分散は )とします。
歪度,尖度の定義について
歪度,尖度の定義について
- 分布の特徴を表す指標としては平均 や分散 が有名ですが,それだけではありません。この記事では歪度,尖度という量を紹介します。
- 平均や分散が存在しない分布がある(→コーシー分布とその期待値などについて)ことからも分かるように,歪度や尖度が存在しない分布もあります。
- 尖度に がついているのは正規分布の尖度が になるように調整するためです。尖度の定義に をつけない流儀もあります。
歪度の意味
歪度の意味
歪度(わいど)は平均まわりの三次モーメントを標準偏差で正規化したもので, 分布の歪み具合(どれくらい非対称なのか)を表します。
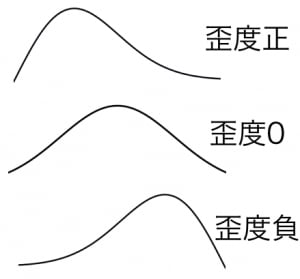
(単峰型の分布について,一般的に)
歪度が正のときやや左側にコブがあり,
歪度が のとき左右対称
歪度が負のときにやや右側にコブがあります。
平均から遠いところが に大きく寄与するので,
左側にコブがある
右側に大きく離れたやつがいる
となりやすいわけです。
尖度の意味
尖度の意味
尖度(せんど)は平均まわりの四次モーメントを標準偏差で正規化したものです。分布の尖り具合,あるいは分布の裾の重さを表す指標だと説明されることが多いです。
ただ,これらの説明は少々納得しがたいです。
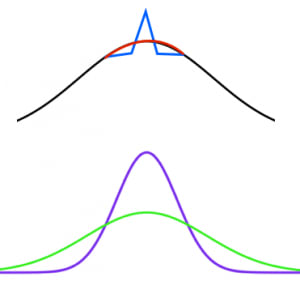
・「尖度は尖り具合を表す」に対する反論
分布のピーク部分の形状が丸くても尖ってても尖度にはほとんど影響がない(図はやや極端な例だが,真ん中部分が赤線でも青線でも尖度はほぼ同じ)。
・「尖度は裾の重さを表す」に対する反論
定数倍の操作で不変(後述)なので分布を縦に押しつぶしても(横に広げても)尖度の値は変わらない(緑と紫の尖度は同じ)。
というわけで,尖度の感覚的な意味は私もよく分かりません。単純に「平均まわりの四次モーメントを標準偏差で正規化したもの」と理解しています。
2016/7/20 追記:読者の方から以下のご指摘がありました。
-
大雑把には「尖る」は 平均近傍に分布が集中し,かつ,裾が重くなるという意味。
-
上の一つ目の反論の例については,先端の一部分のみが尖っても「尖る」の意味に「裾の重さ」も含まれるため,それだけでは尖度が変わらない場合もある,と理解できる。
-
上の定数倍の例は,裾が軽くなっても,その分が平均近傍に集中し,平均近傍が細く高く伸び,差し引きで変わらない,と理解できる。
一次変換に関して不変
一次変換に関して不変
歪度,尖度は で正規化しているため, 定数倍や平行移動で値が変わりません。
が従う分布の歪度,尖度は が従う分布の歪度,尖度と等しい。
平行移動と定数倍で が不変であることを示します。
・平行移動について
平行移動しても , の値はともに変わらない。
・定数倍について
確率変数 に対して を考えると,
また,標準偏差は 倍されるので も 倍される。
尖度の感覚的な意味とその理論的な説明(そんなものないのかもしれませんが)をご存知の方はご一報ください!→ご一報ありがとうございました!











