高校数学の美しい物語
更新
当サイト発の書籍など
当サイト発の書籍など
- 問題集(PDF):
サイトの各ページと対応している問題集です。
→高校数学の問題集 ~最短で得点力を上げるために~ - 中学数学の本:
→超ディープな中学数学の教科書 - 算数の本:
→超ディープな算数の教科書 - 高校数学の本:
→【書籍】高校数学の美しい物語
3次関数の極大値と極小値の差をすばやく計算するテクニック
3次関数の極大値と極小値の差をすばやく計算するテクニック
が極大値と極小値を持つとき,その差は である。ただし, は の解。
行列の最小多項式
行列の最小多項式
行列 の最小多項式とは,最高次数の係数が の多項式 であって となるもののうち次数が一番小さいものである。
この記事では,線形代数においてとても重要な最小多項式について解説します。
多様体入門1~定義と簡単な例
多様体入門1~定義と簡単な例
多様体とは,局所的にユークリッド空間 と微分同相になる空間である。
次の2つがポイントである。
- 球など曲がった図形をユークリッド空間と見なすことができる。
- 微分を考えることができる。
この記事では多様体の定義と簡単な例を紹介します。
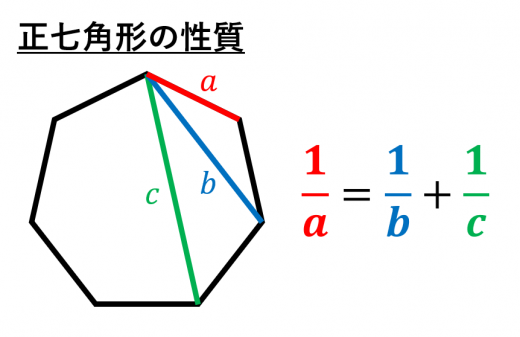
正七角形の対角線の性質
正七角形の対角線の性質
レルヒの公式
レルヒの公式
微分と極限の交換
微分と極限の交換
- は 上の微分可能な関数列で に収束
かつ
- は 上で一様収束
ならば, となる。つまり,微分と極限が交換できる。
この記事では,微分と極限の交換についての例や定理を見ていきます。
ディガンマ関数
ディガンマ関数
ディガンマ関数 とは,ガンマ関数の対数微分,すなわち のことである。
ディガンマ関数は,ガンマ関数の対数微分によって得られる特殊関数です。
この記事では,ガンマ関数を通してディガンマ関数の様々な性質を見ていきます。
ガンマ関数の無限積表示と相反公式
ガンマ関数の無限積表示と相反公式
に対して,ガンマ関数を と定義することができる。
ガンマ関数とゼータ関数の解析接続
ガンマ関数とゼータ関数の解析接続
ラマヌジャンのタクシー数
ラマヌジャンのタクシー数
は2つの立方数の和として2通りに表される最小の自然数である: これを(ラマヌジャンの)タクシー数という。
この記事では,ラマヌジャンのタクシー数を紹介します。
素因数の数の評価~京大特色2023
素因数の数の評価~京大特色2023
以上の自然数 に対して, を割り切る素数の個数を とする。例えば のとき, を割り切る素数は と と なので, である。不等式 を満たす 以上の自然数 をすべて求めよ。
京大の特色入試の問題を解説します。
オイラーの定数γの意味と東大の過去問
オイラーの定数γの意味と東大の過去問
をオイラーの定数(オイラー・マスケローニ定数)といいます。
という無限級数(調和級数)は,だいたい と同じスピードで発散します。この2つの差の極限がオイラーの定数です。
線型汎関数と双対ベクトル空間
線型汎関数と双対ベクトル空間
を実ベクトル空間とする。
への線型写像 を線型汎関数という。
線型汎関数の集合を と定める。
に和とスカラー倍を以下のように定めると, はベクトル空間になる。
を の双対ベクトル空間という。
※ 和の単位元は任意の を に送る線型写像である。
※ 複素ベクトル空間に対しても から への線型写像の集合を考えれば双対ベクトル空間が得られる。
ハウスドルフ空間
ハウスドルフ空間
位相空間 がハウスドルフ空間であるとは,任意の異なる2点 に対して,ある開近傍 , であり となるものが存在することである。

この記事では,位相空間論において重要なハウスドルフ空間を解説します。
正多角形の対角線の長さの偶数乗和と積
正多角形の対角線の長さの偶数乗和と積
正 角形 が半径 の円に内接しているとき,以下の1~4が成立する。
3 で とすると1になります。
正方形の例で式の意味を確認したあと,1~4を証明していきます。
ピックの定理
ピックの定理
頂点がすべて格子点上にある多角形の面積は
内側の格子点数+辺上の格子点数
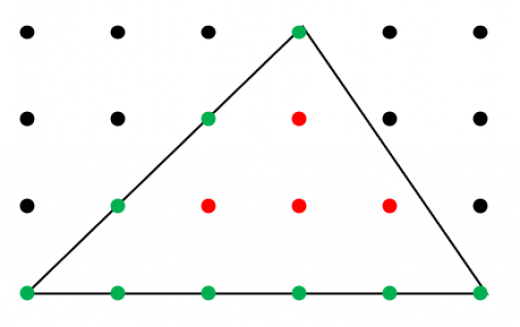
ピックの定理は,多角形の面積と格子点の数の間の関係を示す定理です。ピックの定理の意味・例・証明を紹介します。
ディオファントス近似にまつわる入試問題
ディオファントス近似にまつわる入試問題
実数 に対して, を満たす整数 を探すという問題を ディオファントス近似 といいます。
この記事ではディオファントス近似にまつわる入試問題をまとめました。
是非チャレンジしてみてください。
東大数学の過去問まとめ
東大数学の過去問まとめ