解答
AB=∣1−z∣
BC=∣z−z2∣=∣z∣⋅∣1−z∣
CA=∣z2−1∣=∣1+z∣⋅∣1−z∣
よって,AB:BC:CA=1:∣z∣:∣1+z∣
(
角度は辺の長さの比のみで決まる)
鋭角三角形になる条件は,
AB2+BC2>CA2
BC2+CA2>AB2
CA2+AB2>BC2
つまり,z=a+bi
(a,b
は実数)とおくと,
12+a2+b2>(1+a)2+b2
a2+b2+(1+a)2+b2>1
(1+a)2+b2+1>a2+b2
これを整理すると,
a<0
(a+21)2+b2>41
a>−1
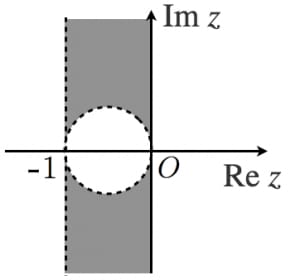
答えは図のグレーの部分(境界は全て除く)。
別解
(こちらの方がスタンダートと思われる)
z=1
は不適。
z=a+bi
とおく。
角
A
が鋭角より,
−2π<arg(z−1z2−1)<2π
よって,a>−1
同様に,角
B
が鋭角より,a<0
角
C
が鋭角より,(a+21)2+b2>41
注:3点が同一直線上にある場合,偏角のどれかが
π
になります。つまり,上の条件のどれかを満たしていないのできちんと排除できています。












