中間値の定理の意味と多変数関数への応用
で連続な関数
を考える。
と
の間にある任意の実数
に対して,
となる
が存在する。
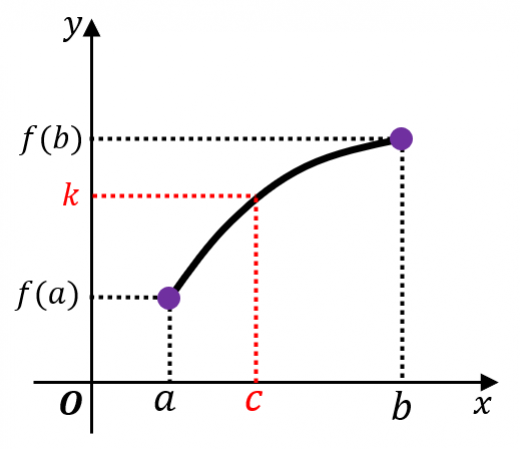
中間値の定理の意味
中間値の定理の意味
中間値の定理の意味はグラフを描けばわかります。大雑把に言うと2点 を結ぶような曲線は必ず赤い直線と交わるという定理です。
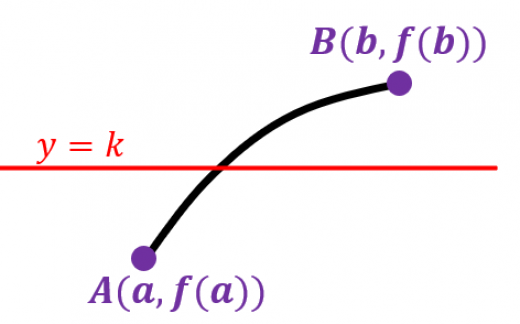
交点が となる点 です。
たしかに赤い直線を横切らずに と を結ぶことはできないので当たり前の定理です。
例
例
まずは,三角関数が登場する簡単な例題です。
方程式 の解が, の範囲に存在することを示せ。
は連続である。
は, と の間にあるので中間値の定理より の解が の間に存在する。
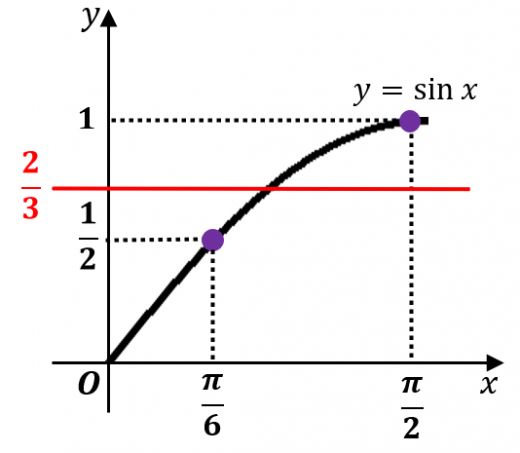
このように,中間値の定理を使うことで方程式に解が存在することを証明できます。
なお,入試問題では特に「 ならば となるような が と の間に存在する」という形で頻出です。
応用問題
応用問題
これ以降はかなり難しい話です。
中間値の定理の多変数関数への拡張を考えるために以下の数オリの問題(を少し変えたもの)を考えてみます:
を満たす任意の非負実数 に対して,
のとりうる値が 以上 以下のすべての実数であることを示せ。
-
であることの証明は省略します。気になる方は→1984年IMO第1問の解説
-
ここでは, が 以上 以下の値を全てとりうることを中間値の定理で証明してみます。 は多変数関数なのでうまいこと一変数関数に変換してから中間値の定理を使います。
は で最小値 , で最大値 を取ることに注意して,
の一変数関数 を
と定義する。
は連続。
よって,一変数関数の中間値の定理が使えて,
任意の実数 に対して
となる が と の間に存在する。
よって,
とすれば を満たし, となる。
よって から まで全ての値をとりうる!
多変数関数の中間値の定理
多変数関数の中間値の定理
さきほどの例を一般化してみます。二変数関数 に対する中間値の定理です!三変数以上でも全く同様です。
- は連結な領域 上で定義されている。つまり定義域内の任意の2点 と に対してそれを結ぶ曲線 がある。
- は連続。
このとき, と の間にある任意の実数 に対して, 上の点 で を満たすものが存在する。
さきほどの数学オリンピックの例を一般化するだけで全く同様にして証明できます。
イメージは一変数の場合と同じです。
「高さの違う2点を結ぶとき,どんな道を通ってもその中間の高さを絶対に一回は横切る」
「高さ」とは関数値のことです。

図の説明:山の地図だと思ってください。 が出発点。 が山頂。登るルート として青い線を選んでも赤い線を選んでもOK。水色の領域が定義域 。山頂を目指すときにどういうルートで登っても任意の標高を一回は通過する!
関連する話題
関連する話題
-
混同しやすい別の定理として平均値の定理があります。→平均値の定理の意味・証明・応用例題2パターン
-
が多項式の場合に,ある意味で中間値の定理よりも強い定理として「デカルトの符号法則」があります。→デカルトの符号法則
-
中間値の定理が数学オリンピックの問題で活躍した例もあります。→ラグランジュの補間公式とその応用例の応用例2
多変数関数は大学に入ってから本格的に学びますが,一変数関数のときのイメージが非常に重要です。











