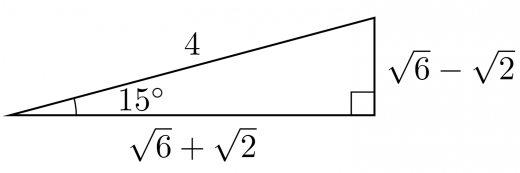sin15∘ の計算方法を3通り紹介します。
加法定理
45∘−30∘=15∘ に注意して加法定理を用いましょう。
導出1. 加法定理
sin15∘=sin(45∘−30∘)=sin45∘cos30∘−cos45∘sin30∘=22⋅23−22⋅21=46−2
半角の公式
15∘=21×30∘ に注意して半角の公式を用いましょう。
導出2. 半角の公式
半角の公式より
cos30∘=1−2sin215∘
である。cos30∘=23 より
sin15∘=42−3=22−3=224−23=223−1=26−2
となる。
なお,下から2つめの等式は 二重根号の外し方・外せないものの判定 を参照のこと。
初等的な計算
導出3
下図のような直角三角形を考える。
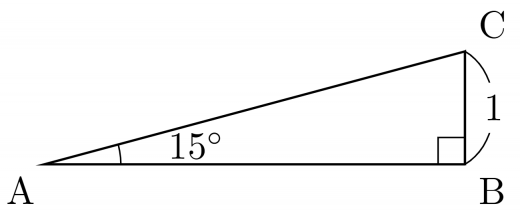
∠DCA=15∘ となるように AB 上に D を取る。(下図参照)
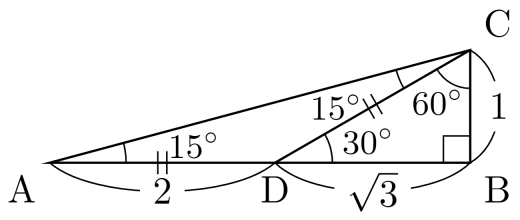
∠DAC=∠DCA=15∘ より AD=CD である。
また,この時 △BCD は 30∘,60∘,90∘ の三角形であるため,BD=3,AD=CD=2 である。
以上より
AC=AB2+BC2=(2+3)2+12=8+43=6+2
と計算されるため
sin15∘=6+21=46−2
となる。