なぜ定積分で面積が求まるのか
更新
と および 軸で囲まれた部分の面積は, という定積分で計算できる。
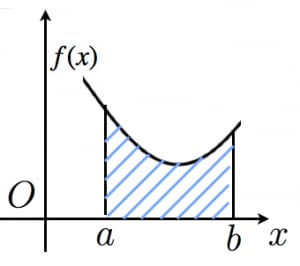
(ただし, において とする)
定積分とは
定積分とは
面積について考える前に,そもそも定積分 の意味を確認します。
とは, のこと
ただし, は微分すると になる関数。
を計算しよう。 は微分すると になるので,
定積分で面積が求まる理由
定積分で面積が求まる理由
定積分の定義を確認したところで,図の面積が で計算できることを証明します。

と 軸で囲まれた部分の面積を とおく。

を少し大きくして としたときに がどれくらい変化するか考えると,図より,
ただし, は から 内の の最小値で は最大値。
各辺を で割る:
ここで,各辺 の極限を取る。左辺と右辺は に収束し,中辺は微分の定義より 。
よって,はさみ打ちの原理より,
本質的な部分はここまでです。遂に微分と面積が結びつきました。
あとは,積分定数の部分を調整して証明を完遂します。
上式の両辺を積分して,
ただし, は積分定数。
また, なので を代入して が分かる。
求める面積は の場合なので
微分積分学の基本定理
微分積分学の基本定理
さきほどは定積分を
で定義しました。その結果,
は図の面積である

という定理が証明できました。一方,大学の教科書では「面積」を使って定積分を定義することが多いです(正確には「面積」というより「リーマン和」というものを考える)。つまり,大雑把に言うと
とは図の面積のことである
と定義するのです。この定義をもとに議論すると,逆に
が定理として導けます。これを微分積分学の基本定理と呼びます。つまり,定積分には微分の逆・面積という2つの同値な定義があると言えます。微分の逆と面積が同じというのはおもしろいです。
面積が定積分(=微分の逆演算)で求まるというのは驚くべき事実です。










