y=tanxのグラフといろいろな性質
という関数について,グラフおよび基本的な性質(グラフを描く際に意識すべきポイント)をまとめました。
三角関数のグラフの特徴と簡単な書き方 も合わせてご覧ください。
なお, ではなく のように という文字で登場することも多い関数です。
のグラフ( のグラフ )
のグラフ( のグラフ )
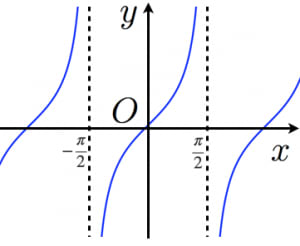
のグラフは図のようになります。
実際にグラフを描く際には意識すべきポイントがいくつもあります。以下の性質を一つでも破るようなグラフを描かないように注意して下さい。
についての基本的な性質
についての基本的な性質
定義域,値域
の 定義域は の奇数倍を除く任意の実数です。 値域は任意の実数です。
周期
の 周期は です。
実際( が定義されるような)任意の実数 について が成立することから の周期は 以下であることが分かります。さらに の範囲で は同じ値を二度は取らないことから周期が 以上であることが分かります。
よって, のグラフを描く際は の範囲でグラフを描いてそれをコピーしていけばOKです。よって,以下では の範囲での のふるまいを考えます。
単調性
の範囲では が増加すると も増加します( 狭義単調増加)。
漸近線
が に下から近づくとき, は限りなく大きくなります。
が に上から近づくとき, は限りなく小さくなります。
よって, は を漸近線(グラフが限りなく近づく直線)に持ちます。
同様に(または周期性から) ( は任意の整数)という直線は の漸近線であることが分かります。
グラフを描く際には漸近線は点線で描くとよいでしょう。
さらなる性質
さらなる性質
以下の性質を破るようなグラフを描いても減点されないこともありますが,分かっている人が見たら不自然ですのでこれらの点にも注意してください。
奇関数
は奇関数,つまりグラフが原点に関して対称です。実際( が定義されるような)任意の実数 について が成立します。
導関数のふるまい
では の導関数 は単調減少です。原点に近づくにつれて接線の傾き(変化の割合)が徐々に緩やかになります。
同様に では の導関数は単調増加です。原点から離れるにつれて接線の傾き(変化の割合)が徐々に急になります。
原点付近でのふるまい
の での微分係数は です。よって, 原点での接線の傾きは です。原点での接線の傾きが に近いようなつぶれたグラフを描かないように注意しましょう。
注: での接線が と平行になるように,という意味です。「必ず に」という意味ではありません( 軸方向と 軸方向の縮尺が違う場合もある)。
サイン,コサインのグラフよりもタンジェントのグラフをきちんと描けない人が多い気がします。











