収束半径の意味と求め方
更新
べき級数 に対して,以下の1,2を両方満たす (ただし )が存在する:
- ならこのべき級数は収束
- ならこのべき級数は発散
このような をべき級数の収束半径と言います。
この記事では は複素数を表すものとします(実数と考えても差し支えありません)。
収束半径について
収束半径について
べき級数が収束するか発散するかにはしきい値が存在します。このしきい値が収束半径です。複素数平面で考えると「半径」の意味が分かります。
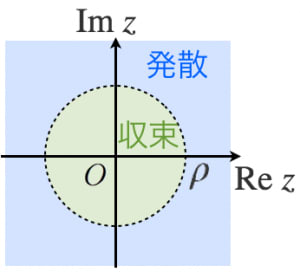
( 以外の)全ての に対して発散するようなべき級数の収束半径は です。
全ての に対して収束するようなべき級数の収束半径は と考えます。
なお,ギリギリの点,つまり の場合にべき級数が発散するか収束するかはケースバイケースです。
冒頭の定理の証明は解析学の教科書を参照して下さい(難しくありません)。
収束半径の例
収束半径の例
べき級数 の収束半径 を求めよ。
注:この例ではギリギリの点,つまり の場合も発散します。
収束半径の求め方
収束半径の求め方
収束半径の求め方を紹介します。
ダランベールの判定法
が存在すれば,収束半径は である。ただし とみなす。
が激しく減少する→
は小さい→収束半径は大きい
という感じです。例えば, が公比 の等比数列の場合は は公比 の等比数列になるので「 が収束半径になる」ことはすぐわかりますね。
べき級数 の収束半径 を求めよ。
であるので ,収束半径も
べき級数 の収束半径 を求めよ。
であるので,
となり 。よって収束半径は
注意点
ダランベールの判定法は が存在するときしか使えません。
べき級数 の収束半径 を求めよ。
より ですが,これは振動するため,極限を持ちません。
このようなケースはどうすればよいでしょうか。
コーシーのべき根判定法
とおくと,収束半径は である。
ただし とみなす。
は 上極限 です。
上極限は,多くの場合ただの と同じ値ですが, のような振動する関数に対しても値が定まります。詳しくは limsup、liminfの意味(数列・集合の上極限・下極限) を参照してください。
であるので,
よって収束半径は
少々形を変えてみましょう。
べき級数 の収束半径 を求めよ。
であるので,
よって収束半径は
収束についての補足
収束についての補足
収束半径の定義では「各 で無限級数が収束するか」を考えています。つまり「各点収束」の考え方です。
実は,より強く「収束半径内では一様収束する」ことが知られています。→各点収束と一様収束の違いと具体例
解析の記事は証明を書くのが難しいので,定理の主張や使い方を中心に解説しようと思います。











