瞬間部分積分のやり方と例題2問
更新
瞬間部分積分は複数回部分積分が必要な問題を素早く解く方法です,めんどうな計算をかなり省略できます,オススメ!
瞬間部分積分のやり方
瞬間部分積分のやり方
2つの関数の積の積分 を求めたい。そして, を何回か微分すれば になる。というような問題に対して有力な方法です。
慣れたら本当に素早く計算できます。
1:三列の表をつくる。二列目に上から と になる手前まで格納する。
2:三列目に上から の積分, の二階積分, と格納する。
3:一列目に上から と交互に格納する。
4:横にかけて縦に足す。

例えば, という不定積分は部分積分を二回行わないと解けません。
そこで, として瞬間部分積分を用います。
二列目はどんどん微分(赤い矢印),三列目はどんどん積分(青い矢印)しています。
この表より, であることが分かります(積分定数を忘れないように)。
多項式×三角関数の積分
多項式×三角関数の積分
次はより複雑な例です。単純な部分積分だけではかなり大変な計算です。
を計算せよ。
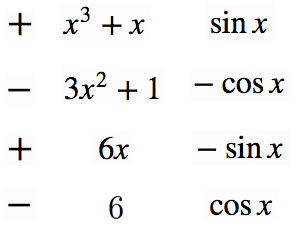
として瞬間部分積分を用います。
三列目の一行目は でなく の積分であることに注意してください。
答えは,
となります。
→高校数学の問題集 ~最短で得点力を上げるために~のT7も参照してください。
瞬間部分積分の証明
瞬間部分積分の証明
瞬間部分積分によって実際に不定積分が計算できていることを確認します。
となる最小の を とおく。 を 回不定積分したものを とおく。
このとき瞬間部分積分をした結果の式は と表される。これを とおく。 の微分が になることを確認すればよい。
こうして証明がなされた。
瞬間部分積分に関する諸注意
瞬間部分積分に関する諸注意
-
瞬間部分積分は部分積分を繰り返し用いるときに不要な手順をカットしたものに過ぎません。よって,瞬間部分積分が正しいことの証明は部分積分を繰り返し用いるだけです。
-
「瞬間部分積分」という言葉はそれなりに有名ですが,一般的ではありません。山本先生(昔の代ゼミ講師)という方が名づけたらしいです。そのため,記述式の答案で「瞬間部分積分」という文言は出さないほうがよいです。
-
瞬間部分積分で積分結果を求めた上で,記述式の答案には「部分積分を繰り返し用いると以下のようになる」と書き,いきなり積分結果を載せればよいです。
-
瞬間部分積分は当然ながら不定積分だけでなく定積分でも使えます。
-
対数関数×多項式の積分は部分積分一発でできるので瞬間部分積分の出る幕ではありません。
部分積分は圧倒的に計算ミスをしやすい問題なので,できるだけ省エネしましょう。











