特異値分解の定義，性質，具体例

特異値分解とは，$m\times n$ 行列 $A$ を $A=U\Sigma V$と分解することです。ただし，

• $U$ は $m\times m$ の直交行列（各列が互いに直交する行列 →直交行列の定義と性質）
• $V$ は $n\times n$ の直交行列
• $\Sigma$ は図のような行列 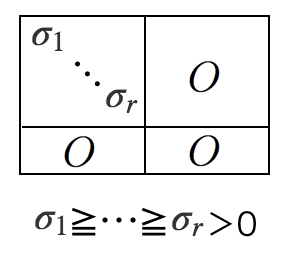つまり「非対角成分は $0$，対角成分は非負で大きさの順に並んだ行列。

です。任意の行列はこのように分解できます。また，$\Sigma$ の対角成分で $0$ でないもの（$0$ を含めることもある）を特異値と言います。

$A=\begin{pmatrix}2&2&2&2\\1&-1&1&-1\\-1&1&-1&1\end{pmatrix}$ の特異値分解（の1つ）は，

$$A= \begin{pmatrix}1&0&0\\0&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\0&-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}\begin{pmatrix}4&0&0&0\\0&2\sqrt{2}&0&0\\0&0&0&0\end{pmatrix}\begin{pmatrix}\frac{1}{2}&\frac{1}{2}&\frac{1}{2}&\frac{1}{2}\\\frac{1}{2}&-\frac{1}{2}&\frac{1}{2}&-\frac{1}{2}\\\frac{1}{2}&\frac{1}{2}&-\frac{1}{2}&-\frac{1}{2}\\\frac{1}{2}&-\frac{1}{2}&-\frac{1}{2}&\frac{1}{2}\end{pmatrix}$$

です。よって，$A$ の特異値は，$4$ と $2\sqrt{2}$ です。

なお，上の等式が正しいこと，および右辺の1つ目と3つ目の行列が直交行列であることは簡単な計算で確認できます。

• $A$ が与えられたとき，特異値を定める行列 $\Sigma$ は一意に決まりますが，直交行列 $U,V$ は一意に定まるとは限りません。

• 行列の（$0$ でない）特異値の数は，その行列のランクと一致します。→行列のランクの意味（８通りの同値な定義）

• 「行列の特異値の二乗和」は「その行列の全成分の二乗和」と等しいです。さきほどの具体例ではどちらも24になっています。この値の平方根を行列のフロベニウスノルムと言います。→行列のフロベニウスノルムとその性質）

• 行列の固有値分解は正方行列に対してのみ定義されますが，特異値分解は正方行列でなくてもできます。

• $A$ が対称行列のとき，$A$ の固有値と特異値は一致します。対称行列は直交行列で対角化できるからです。→対称行列の固有値と固有ベクトルの性質の証明

• 「$A^{\top}A$ の $0$ でない固有値の正の平方根」は $A$ の特異値です。理由は，$A=U\Sigma V$ と特異値分解できるとき $A^{\top}A=V^{\top}(\Sigma^{\top}\Sigma) V$ と固有値分解できるからです。同様に，$AA^{\top}$ の $0$ でない固有値の正の平方根も $A$ の特異値です。後ほどもう少し詳しく説明します。