正方形の頂点と最短距離
正方形の4頂点を結ぶ方法で,使う線分の長さの総和が最も短いものを求めよ。
正方形以外の場合にも拡張できますが,正方形の場合の結果が特に有名な問題です。
シュタイナー木問題
シュタイナー木問題
いくつかの点が与えられた時に,その点たちをうまく連結させることを考えます。
連結させるときに使う線分の長さの和が最小になるような方法を求める問題を,シュタイナー木問題と言います。
- 例えば,点たちを「都市」,連結させるときに使う線分を「道路」と考えると,いくつかの都市を結ぶ最短の道路網を構成する問題になります。
- 例えば,1つの点を発電所,残りの点たちを「家」,連結させるときに使う線分を「電線」に見立てると,使う電線の長さ最小で家々に電気を配給する問題になります(電柱は何本使っても構いません)。
三点の場合のシュタイナー木問題
三点の場合のシュタイナー木問題
本題に入る前に,3点 を結ぶシュタイナー木問題考えます。
が最大だとしても一般性を失いません(このとき が三角形 の最大辺となる)。
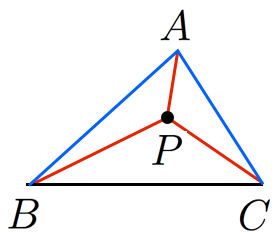
素朴に思いつくのは線分 を引く方法ですが,実は三角形の内部にうまく点 を選んで を結ぶとより短くできる場合があります。つまり, となる場合があります。(図において青線で結ぶより赤線で結ぶ方がお得!)
が 未満の場合, をフェルマー点( を満たす点)に取れば線分和が最小になることが知られています。→三角形のフェルマー点の3通りの証明
- 最大角が 以下なら,フェルマー点と3頂点を結んだもの
- 最大角が 以上なら,短い2辺を使うもの
以下ではフェルマー点の結果をもとに正方形の問題を考えます。
正方形の頂点を最短距離で結ぶ
正方形の頂点を最短距離で結ぶ
次は,正方形の4頂点を結ぶ場合を考えます。
 愚直な方法:一辺が1の正方形の三辺を選んで結ぶと長さの和は3になります。
愚直な方法:一辺が1の正方形の三辺を選んで結ぶと長さの和は3になります。
少し工夫した方法:真ん中に分岐点を1つ作って 型に結ぶと長さの和は になります。

さらに工夫した方法: 型の図の下側の三角形と上側の三角形に注目してそれぞれフェルマー点に分岐点を作ります。結果的に分岐点は2つになります。分岐点の周りの角度が全て であることに注意して長さの総和を計算すると となります。
緑の図が最短であることの証明
緑の図が最短であることの証明
実際に の解が最短であることを,以下の手順で証明します。
- 分岐点は2つ以下のものだけを考えれば十分
- 分岐点を2つに限れば のものが最短
1はグラフ理論の言葉を使います。→グラフ理論の基礎
最適解における,4つの頂点と 個の分岐点をつないだグラフを考える。
このグラフは連結であり閉路を持たない(閉路があったら辺を1本除けるので最適ではない)ので木である。
木において辺の数は頂点の数 なので辺の数は である。
また,各分岐点には 本以上の辺が接続されている(もし2本以下なら余分な頂点なので除去できる)。
よって辺の数は 以上である。
以上より
つまり
2はフェルマー点の導出方法を知っていれば比較的簡単に思いつく方法です。
つの分岐点 がそれぞれ と につながっているとしても一般性を失わない。
正方形 の上側に ,下側に を と が正三角形になるようにとる。

また, と が正三角形になるように を取る。
三角形のフェルマー点のときと同様な議論により
線分和
これは と を結ぶ折れ線の長さなので, を調節して直線になるときが最短となる。実際 の周りの角度が全て のとき直線になる。
正方形のシュタイナー木は非常に有名なのでぜひ覚えておきましょう。











