サラスの公式は大学受験でも活躍します。四面体の体積をすばやく計算できます。
四面体の体積を求める公式
座標空間上の4点
O(0,0,0),A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)
に対して四面体
OABC
の体積は,
61∣y1z2x3+z1x2y3+x1y2z3−z1y2x3−x1z2y3−y1x2z3∣=61∣∣det⎝⎛x1x2x3y1y2y3z1z2z3⎠⎞∣∣
つまり,以下の手順で体積が計算できます!
- 座標を並べた行列 X=⎝⎛x1x2x3y1y2y3z1z2z3⎠⎞ を書く
- その行列式 detX をサラスの公式で計算する
- 最後に 61 倍する。
例題
例題2
O(0,0,0),A(0,1,2),B(3,4,−3),C(−2,−1,0) のとき,四面体 OABC の体積を計算せよ。
解答
-
X=⎝⎛03−214−12−30⎠⎞ の行列式を計算すればよい。
-
サラスの公式を使って計算すると,例題1で計算したように 16 になる
-
よって体積は,616=38
面積を求める公式
四面体の体積は3×3行列の行列式で表せました。同様に,三角形の面積は2×2行列の行列式で表せます。
三角形の面積求める公式
座標平面上の3点
O(0,0),A(x1,y1),B(x2,y2)
に対して,三角形
OAB
の面積は,
21∣x1y2−y1x2∣=21∣∣det(x1x2y1y2)∣∣
原点が含まれない場合
面積or体積を求めたい図形の頂点に原点が含まれない場合は,いずれかの頂点が原点に重なるように全ての頂点を平行移動して考えます。
例
A(1,3),B(−1,−3),C(0,−1)
として三角形
ABC
の面積を求めたいときは,各頂点を
y
方向に1ずらして
A′(1,4),B′(−1,−2),C′(0,0)
として
三角形
ABC
の面積=三角形
A′B′C′
の面積
=21⋅(−2)−4⋅(−1)=1
,
とすればよい。
面積・体積公式の応用例としては,以下があります。
四面体の体積を求める公式の証明
愚直に体積を計算していく方針ですが,座標空間の便利な道具を駆使することで簡単な計算で証明できます。
使う道具は以下の3つです:
証明
三角形
OAB
を底面とする四面体と見て体積を計算する。
三角形
OAB
の面積
S
は,
S=21OA×OB×sin∠AOB=21OA×OB×1−cos2∠AOB=21OA2OB2−(OA⋅OB)2=21(x12+y12+z12)(x22+y22+z22)−(x1x2+y1y2+z1z2)2=21(y1z2−y2z1)2+(z1x2−z2x1)2+(x1y2−x2y1)2
次に,三角形
OAB
を含む平面の方程式を求める。法線ベクトルはベクトルの外積を用いて,
OA×OB=(y1z2−y2z1,z1x2−z2x1,x1y2−x2y1)
と表せるので,求める平面が原点を通ることに注意すると,
(y1z2−y2z1)x+(z1x2−z2x1)y+(x1y2−x2y1)z=0
となる。
最後に三角形
OAB
と点
C
の距離
h
を求める。点と平面の距離公式より,
h=(y1z2−y2z1)2+(z1x2−z2x1)2+(x1y2−x2y1)2∣(y1z2−y2z1)x3+(z1x2−z2x1)y3+(x1y2−x2y1)z3∣
ここで,求める体積は
31Sh
だが
S
と
h
の分母が打ち消し合って
h
の分子の
61
倍が残り,証明された。
なお,この公式を応用することで六辺の長さから四面体の体積を求める公式も導出できます。→四面体の体積を求める2つの公式with行列式
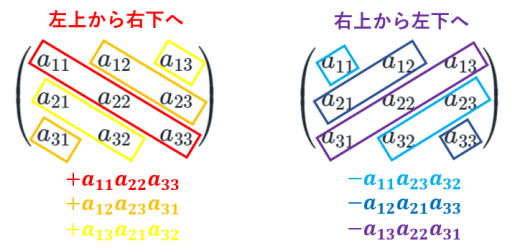
サラスの公式で計算するときは「右端と左端はつながっているいわゆるドラクエスタイル」をイメージするとよいです。
Tag:大学入試共通テストにも役立つ即効性の高い公式まとめ
Tag:三角形の面積を求める公式まとめ