ラムゼーの定理と6人の問題
6人いると「互いに知り合いである3人組」か「互いに知らない3人組」が存在することを証明せよ。
「パーティー問題」「Theorem on friends and strangers」などとも呼びます。
数学オリンピックではこのような問題を解けることが大事になります。数オリに出ない人も非常に有名な問題なので知っておくとよいでしょう。
問題の解答
問題の解答
言葉で表現すると大変なのでグラフを用います。つまり,6人をそれぞれ点で表し,知り合いを赤い線で結び,知らない人を青い線で結びます。このグラフにおいて赤い三角形か青い三角形が存在することを示せばよいです。
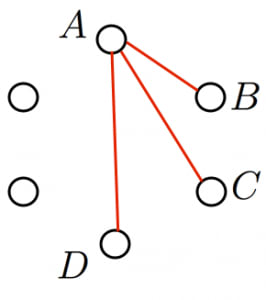
1つの点 に注目すると,5本枝が出ているので,そのうち3本以上は同じ色である。赤が3本以上出ているとして一般性を失わない。その相手を とする。
- を結ぶ枝が赤→ が赤い三角形
- を結ぶ枝が赤→ が赤い三角形
- を結ぶ枝が赤→ が赤い三角形
- 上記のいずれでもない→ が青い三角形
となり,いずれの場合も赤い三角形または青い三角形が存在することが分かる。
このようにグラフを用いると簡潔に表現できます。数学オリンピックでも「記述の道具」としてグラフ理論を知っていると便利です。→グラフ理論の基礎

ちなみに,5人の場合は図のように頑張れば赤い三角形も青い三角形もつくらずにグラフがかけます。
つまり,どの3人に注目しても知り合いである2人も知り合いでない2人も存在します。
ラムゼーの定理
ラムゼーの定理
上記の問題を一般化します。「完全グラフ」とは全ての頂点間に枝が張り巡らされたグラフのことです。
は任意の正の整数とする。頂点数 の完全グラフの枝を赤と青に塗り分けるとき, が十分大きければ 「頂点数 の赤い完全グラフ」または「頂点数 の青い完全グラフ」が必ず存在する。この条件を満たす最小の をラムゼー数と呼び, と表す。
ラムゼー数が無限大に吹っ飛ばずにきちんと存在するというのがラムゼーの定理です。
定理の主張はほとんど自明に思えるかもしれませんが,厳密に示そうとするとけっこう大変なようです。
-
さきほど示したことは ラムゼー数 ということになります。
(パーティー問題の結果が を表しており,頂点数 の場合にうまく塗り分けできることが を表しています。) -
が一般の場合にラムゼー数を求めるのは非常に難しい問題です。
-
塗り分けの色の数を増やしてさらに一般化することもできます。
-
IMO 1964第4問は,六人の問題とその証明を知っていると非常に有利になる問題でした。練習問題にどうぞ!
17人それぞれが他の全員と互いに手紙をやりとりしている.その手紙では三つの話題のみがやりとりされている.そして,同じ二人組の間でなされる話題は常に同じ(一つの)話題である.
このとき,互いに同じ話題の手紙をやりとりした三人組が存在することを証明せよ.
6人の問題の証明はなかなか美しいので個人的に推しています。
Tag:難しめの数学雑学・ネタまとめ











