ピタゴラス数の求め方とその証明
ピタゴラス数 とは, を満たす正の整数の組 のこと。

ピタゴラス数の意味と,ピタゴラス数の求め方についてわかりやすく説明します。
ピタゴラス数とは
ピタゴラス数とは
ピタゴラス数は, を満たす正の整数の組のことです。
-
,つまり なので はピタゴラス数である。
-
他にも なので もピタゴラス数である。
ピタゴラス数と三平方の定理
ピタゴラスの定理(三平方の定理)によると,直角三角形の3辺の長さについて, が成立します。→三平方の定理の4通りの美しい証明
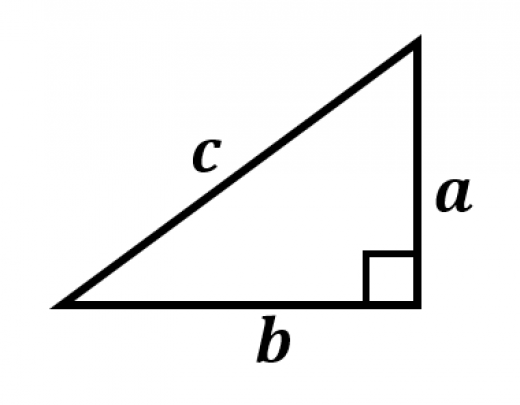
つまり,ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のこととも言えます。
ピタゴラス数を作り出す公式
ピタゴラス数を作り出す公式
正の整数 を用いて,
とすると, はピタゴラス数になります。
この公式を使うと,いくらでもピタゴラス数を作ることができます。
-
とすれば,
-
とすれば,
となり,さきほどのピタゴラス数の例を作り出すことができました。
実際,
なので,
とすれば はピタゴラス数になることが分かります。
では,逆に「全てのピタゴラス数」をこの方法で生み出せるでしょうか?
原始ピタゴラス数とは
原始ピタゴラス数とは
-
ピタゴラス数は,定数倍してもピタゴラス数です。 例えば, はピタゴラス数ですが,それを2倍した や3倍した もピタゴラス数です。
-
定数倍して一致するものは 「同じ」ピタゴラス数とみなしましょう。つまり,最大公約数が のピタゴラス数のみを考えしょう。
-
最大公約数が のピタゴラス数を原始ピタゴラス数と言います。以下では,原始ピタゴラス数について考えます。
全ての原始ピタゴラス数を生み出す
実は,さきほどの公式:
で「全ての原始ピタゴラス数」を作り出すことができます!
ピタゴラス数の中で の最大公約数が のものは,ある正の整数 を用いて
(または )
という形で表せる。
この定理を知っていると,ピタゴラス数にまつわる入試問題の見通しが良くなることがあります。
では,定理を証明してみます。
以下の順番で証明していきます。
-
と のどちらか一方のみ奇数で他方は偶数。 は奇数である。
-
はともに平方数である。
-
定理を証明する。
を原始ピタゴラス数とする。
-
ともに偶数と仮定すると, も偶数となり最大公約数が でなくなるので矛盾。
-
ともに奇数と仮定すると, は で割って 余る。しかし, は平方数であり で割った余りが になることはない( が偶数なら は の倍数, が奇数なら は で割って 余る)。よって矛盾。
つまり, と のどちらか一方のみ奇数で他方は偶数。
よって, が奇数なので も奇数
を奇数, を偶数としても一般性を失わない。
次に2を背理法で証明します。
と のどちらか一方でも平方数でないとすると,それらの積は平方数である( に注意)ので
と は共通因数 を持つ。つまり, ただし は自然数,と書ける。
これを について解くと,
よって, はともに の倍数となり,さらに も の倍数となるので原始ピタゴラス数であるという仮定に矛盾。
最後に整理します。
2より と書けるので,これを について解くと
となり証明完了。
なお,この証明中には整数問題の重要なテクニックが2つ含まれています。
「割った余りを考える(平方剰余)」により1の証明が,
「整数問題の不定方程式は因数分解すべし」により2の証明が自然と思いつくようになれば玄人です。
発展:原始ピタゴラス数の木
この記事の復習に,→高校数学の問題集 ~最短で得点力を上げるために~のT146も参照してください。
ピタゴラス数を全て作り出せるというのはすごい!
Tag:不定方程式の解き方まとめ











