多項式の割り算の二通りの計算方法と例題
多項式の割り算について説明します。そもそも多項式の割り算とは何かを述べた後,割り算のやり方を2通り紹介します。

多項式の割り算の意味
多項式の割り算の意味
まずは,多項式の割り算(整式の除法)の定義です。定義は少しわかりにくいので,後の例と合わせて確認してください。
与えられた多項式 に対して,
を満たす多項式 が1つに決まる。 を商, を余りと言う。
を で割ると,
となるので,商は で余りは
普通の整数の割り算の定義と似ていますね。
与えられた正の整数 に対して,
を満たす 以上の整数 が1つに決まる。 を商, を余りと言う。
多項式の割り算のやり方
多項式の割り算のやり方
多項式 が与えられたときに割り算をする( を求める)2通りの方法を解説します。
方法1:筆算
多項式の割り算も,普通の整数の割り算と似たように筆算でできます。
例題を使って筆算のやり方を解説します。
を で割った商と余りを求めよ。
ステップ1:割る式と割られる式の係数を並べる。
図の上側のように の係数 と の係数 を書きます。存在しない項は係数
とみなすことに注意してください。
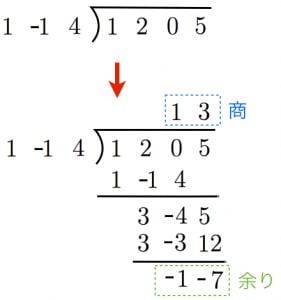
ステップ2:数に対する割り算と同じように筆算する(左の桁を1つずつ消していくように)。
図の下側のように割り算を筆算で実行してください。
ステップ3:右端まで行ったらストップ。上に商の係数が並び,下に余りの係数が並ぶ。
この場合,商の係数は順番に
なので
,
余りの係数は順番に なので と分かります。
方法2:割り算の等式を立てる
次は,割り算の等式: から直接 を計算する方法です。
を で割った商と余りを求めよ。
商を ,余りを とすると より, の次数= の次数+ の次数です。よって, が一次式であることがわかります。
次数に注意しながら恒等式の問題にします。
商 は一次式,余り は一次以下の式なので, とおける。
が恒等式となる を求めればよい。右辺を展開すると,
となる。係数比較すると
これを解くと,
よって,商は ,余りは
-
係数比較の際に, 高次の項の式から順々に見ていくことで が順々に一つずつ決まっていきます。この例題以外でも同じような構造になります。
-
試験では出てきた値をもとの赤字の等式に代入して恒等式であることを再確認(検算)することをオススメします。
二つの方法の比較,例題
二つの方法の比較,例題
-
慣れたら方法1(筆算)の方がかなり早いですが,割り算の意味,構造は方法2(割り算の等式)の方が分かりやすいです。
-
が一次式(特に一次の係数が1)のときは組立除法を使うとさらにスピーディーにできます。
最後に例題をもう一問。
を で割った商と余りを求めよ。
図のように筆算をすると,商は ,余りは
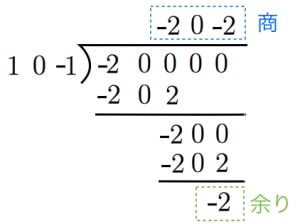
注: なので が4つ並んでいる。
商は二次式,余りは一次以下の式なので,
を満たす 〜 を求めればよい。
係数比較すると となるので商は ,余りは
多項式の割り算は計算ミスしやすいので検算も忘れないようにしてください!










