角の二等分線に関する重要な3つの公式
更新
内角の二等分線の図において,
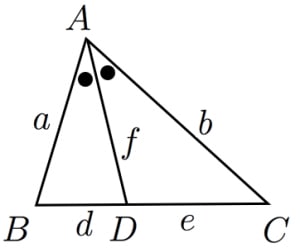
ただし, は の二等分線と の交点で,
内角の二等分線に関して大事な公式を3つ紹介します。辺の比に関する公式1は教科書レベルで,残りの2つの公式はややマニアックです。後半では,外角の二等分線に関する公式も紹介します。内角の場合と比較するとおもしろいです。
二等分線に関する3つの公式について
二等分線に関する3つの公式について
- 公式1は有名な辺の比の公式で教科書にも載っています。覚えましょう。
- 公式2は暗記する必要はありませんが,導出方法は覚えておくとよいです。
- 公式3はスチュワートの定理の特殊な形です。おもしろいですし,応用例も多いです。
これら3つの公式を使うことで,「二等分線を含む三角形について情報が3つ与えられれば残りの情報は全て求まる」ことが分かります。
-
が分かれば公式2により が分かり,余弦定理から も分かります。
-
が分かれば公式1により も分かりさらに公式3から も分かります。
以下では,それぞれの公式の証明と注意点を説明します。
公式1:角の二等分線と辺の比の公式
公式1:角の二等分線と辺の比の公式
まずは, という有名な公式を証明してみましょう。
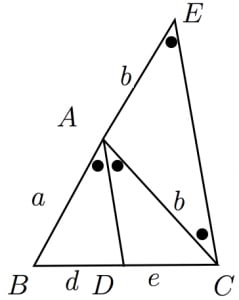
直線 と「 を通り と平行な直線」との交点を とおく。
同位角,錯角より,
よって,
また,3つの角がそれぞれ等しいので三角形 と三角形 は相似であり,
つまり
公式2:面積に注目した二等分線の公式
公式2:面積に注目した二等分線の公式
公式2は公式自体よりも考え方が重要です。数学オリンピックなどの難問では頻出の構図です。三角関数の倍角の公式を使うことで両辺がうまくキャンセルされて綺麗な形になるのがポイントです。

三角形 の面積は
また,三角形 と三角形 の面積の和は,
両者が等しいことと より,
つまり,
公式3:角の二等分線の長さ
公式3:角の二等分線の長さ
角の二等分線の長さは, で計算することができます。これを3通りの方法で証明してみます。

公式2と三角形 についての余弦定理より,
これを について解く:
ただし,最後の変形は公式 による。
三角形 の外接円と の交点を とおく。

円周角の定理より白丸○の角度が等しいので と は相似。
よって,
ただし,最後の等号は方べきの定理を使った。
スチュワートの定理から分かる。→スチュワートの定理の証明とその仲間
外角の二等分線に関する定理
外角の二等分線に関する定理
外角の場合も,内角の場合と似た式が成立します。
同じように, の外角の二等分線と直線 との交点を とします。
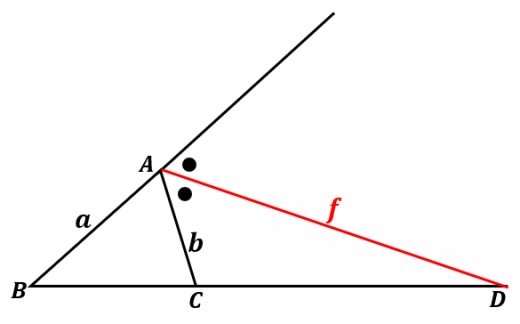
外角の二等分線の図において,
内角の場合の式:
と比べてみるとおもしろいです。証明も,内角の場合とほとんど同じようにできます。
内角の場合と同じく,直線 と「 を通り と平行な直線」の交点を とすると,相似な三角形ができる。
3つの三角形の面積について,
が成立するので
となることからわかる。
3の証明も内角の場合の証明とほとんど同じです。証明1,2のどちらも外角の場合に拡張できて楽しいのでやってみてください。
→高校数学の問題集 ~最短で得点力を上げるために~のT42では,3が活躍する例題と3通りの解法を紹介しています。
重要なのは公式を暗記することではなく,二等分線を含む三角形において情報が3つ与えられれば他の値は求められる,と理解することです。











