三角形の面積比にまつわる公式たち
更新
三角形の面積比,四面体の体積比にまつわる重要な公式を3つ紹介します。
どの公式も有名で公式自体を知っている人は多いでしょうが,大学入試問題の難問や数学オリンピックの証明問題の途中経過にしれっと使われることもあり,実践で使いこなすのは鍛錬が必要です。 この公式が使えそうな形が出てきたら反応できるように頭に叩き込みましょう。
難問に反応して面積比の公式を使いこなすために,数式で公式を覚えるだけではなく 図形的なイメージをインプットしておきましょう。
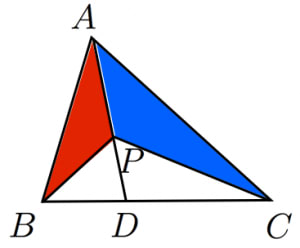
一辺を共有する三角形の面積比の公式
一辺を共有する三角形の面積比の公式
角を共有する三角形の面積比の公式
角を共有する三角形の面積比の公式
図において
△ △

△ △
「角を共有する三角形の面積比は線分の積の比に変換できる」と覚えておきましょう。
この公式の頻出応用例として,
- △ と四角形 の面積比を求める問題も多いです。
- また, と が平行の場合は相似な図形の面積比の公式に帰着されます(これも超頻出です)。
以上2つの頻出系の合体技の例としてブラーマグプタの公式とその証明と2つ目の証明を挙げておきます。
角を共有する四面体の体積比の公式
角を共有する四面体の体積比の公式
「角を共有する三角形の面積比の公式」の空間図形バージョンです。
図において
四面体 四面体

この公式の証明は初等幾何を用いるのが一般的ですし,平面図形バージョンの拡張としてこの公式が成立することは当たり前だと思う人がいるかもしれませんが,ここではあえてサラスの公式を用いて証明してみます。
を原点として以下のように座標を取る。
ただし,
ここで,サラスの公式より
四面体 の体積 四面体 の体積
となり公式は示された。
記号を使うとごちゃごちゃしますが, サラスの公式がきちんと理解できていれば一瞬で分かるエレガントな証明です。
ちなみに,上側の四面体と下側の台の体積比を求める問題も多いです。また,相似な場合は有名な体積比の公式(1:相似比の3乗)となります。→相似比と面積比・体積比:いろいろな例と証明
公式を理解することと使いこなせることには大きなギャップがある
Tag:三角形の面積を求める公式まとめ