一次変換の意味と重要な5つの例(折り返し・回転・対称移動)
一次変換とは,行列
のかけ算による変換です。行列
に対応する一次変換は,
を
に写します。
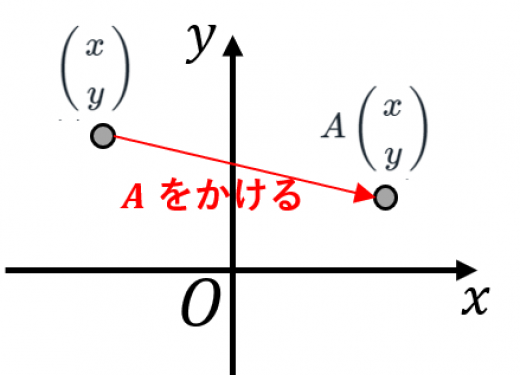
一次変換は,いろいろな例を見ると理解が深まります。この記事では,重要な一次変換を5つ紹介します。
x軸に関する折り返し
x軸に関する折り返し
に対応する一次変換は 軸に関する折り返しを表す。

この変換によって, という点は
に写る。つまり, 座標だけをマイナス1倍する変換なので「 軸に関する折り返し」を表す。
y軸に関する折り返し
y軸に関する折り返し
軸に関する折り返しも同様です。
に対応する一次変換は 軸に関する折り返しを表す。
この変換によって, という点は
に写る。つまり, 座標だけをマイナス1倍する変換なので「 軸に関する折り返し」を表す。
原点に関する対称移動
原点に関する対称移動
に対応する一次変換は原点に関する対称移動を表す。
この変換によって, という点は
に写る。これは,原点に関する対称移動。
行列積と変換の合成
行列積と変換の合成
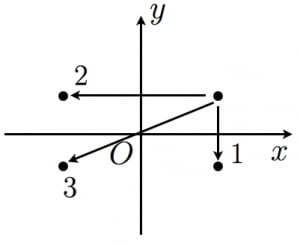
ここまでの結果をまとめます。
-
軸に関する折り返し:
-
軸に関する折り返し:
-
原点に関する対称移動:
-
簡単な計算により, が分かります。これは「 軸に関して折り返してから 軸に関して折り返すのは原点に関して対称移動するのと同じ」ということと対応しています。
-
また, も分かります。これは「 軸に関する対称移動を2回ほどこすと何もしないのと同じ(恒等変換)」などと対応しています。
このように,「行列の積」と「変換の合成」が対応しているので,行列積を計算すると変換の間の意味付けができます。逆に,行列積の計算により,合成変換に対応する行列を求めることができます。
「行列積と変換の合成が対応していること」は線形代数や群論をはじめ大学の数学で大活躍します。
回転行列
回転行列
次は,座標平面での計算で最も活躍する公式の1つです。
に対応する一次変換は原点を中心とした(反時計回りに だけ回すような)回転を表す。
この変換によって, という点は
に写る。ただし,最後の等号は三角関数の加法定理を用いた。
これは,原点を中心に反時計回りに 回転させることを表す。
回転が一次変換で表せるというのは自明ではない驚くべき事実です。
ちなみに,原点以外を回転の中心としたい場合はベクトルを回転すると捉えればよいです。
座標平面上の正三角形
において

回転行列は,斜めの楕円の方程式(特に45度回転) の計算にも登場します。
原点を通る直線に関する折り返し
原点を通る直線に関する折り返し
最後は少し難しいです。
に対応する一次変換は原点を通る(傾きが の)直線に関する折り返しを表す。
さきほど述べた「行列積は合成変換に対応する」という事実が活躍します。
原点を通る傾きが の直線 を, 時計回りに 回転させると 軸と一致する。
よって,「直線 に関する折り返し」は以下の3つの変換の合成:
- 原点中心に 回転(赤色)
- 軸に関して対称移動(緑色)
- 原点中心に 回転(青色)

よって, となる(変換は右からされるので積の順番に注意)。
よって, は,
となる。この行列積を,倍角の公式を用いて計算すると
となる。
特に,回転行列と直線の折り返しは,座標平面を用いてゴリゴリ計算するときに便利です。数学オリンピックなどの難しい図形問題を座標で解くときに計算量を減らす助けになります。
なお,射影も重要な一次変換です。スクリーンに光を当てるようなイメージの変換です。→射影行列のイメージと楽しい公式
一次変換と線形代数
一次変換と線形代数
今回紹介したような2次元座標平面における一次変換に慣れていると,線形代数のいろいろな概念を理解するときに図形的なイメージを持ちやすく,助けになります。例えば,
-
行列式は,変換前の図形と変換後の図形の(符号付き)面積比を表します。今回登場した5つの行列はすべて行列式が なので,面積は変換前と変換後で変わりません。
-
固有ベクトルは,変換で向きが変わらないベクトルです。固有ベクトルの方向を座標軸に取り直すと,変換の意味がわかりやすいです(対角化)。
-
ランク(rank)は「全体」を変換した先の次元です。
大学数学を学んで,行列=一次変換=線形写像の大切さを思い知りました。











