ルモアーヌ点(類似重心)とその性質
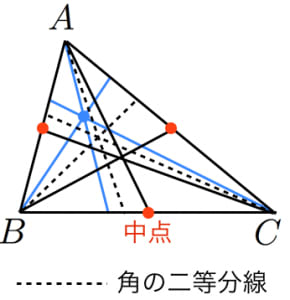
三角形 において,類似中線(中線を角の二等分線に関して折り返した直線)は 本あるが,それらは 点で交わる。
この点をルモアーヌ点(類似重心,Symmedian Point,Lemoine Point)と言う。
なお,
ルモアーヌ点の存在証明
ルモアーヌ点の存在証明
より一般に,以下の定理が成立します。
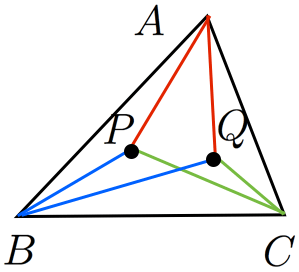
三角形 と点 がある。
角の頂点を通る直線 と角の二等分線に関して対称な直線 を の等角共役線というが, の等角共役線は一点 で交わる。
上の定理において を重心とすれば,ルモアーヌ点の存在が分かります(ルモアーヌ点は重心の等角共役点です)。上の定理の証明は等角共役点とその証明を参照してください。
ルモアーヌ点の性質1
ルモアーヌ点の性質1
本命は後述する性質2です。まずは準備です。
三角形 のルモアーヌ点を とする。このとき,
ただし, は三角形 の面積, は辺 の長さ(他も同様)です。
証明はよい練習問題です。ここでは計算でやってみます。
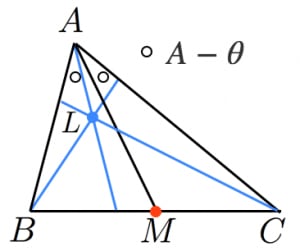
を示す。 の中点を , とおく。
ここで,三角形 に余弦定理および正弦定理を用いると,
これを上式に代入して整理すると,
を得る。
ただし,途中で (中線定理を使えば簡単に導出できる→三角形の五心と頂点までの距離),, を用いる。
ルモアーヌ点の性質2
ルモアーヌ点の性質2
三角形 内の点 から に下ろした垂線の長さを とする。
ルモアーヌ点は を最小にするような点 である。
を3つに分割して考えることにより,
である。よって,シュワルツの不等式より,
よって(シュワルツの等号成立条件から), のときに は最小となる。実際,ルモアーヌ点は(性質1より)この条件を満たしている!
ルモワーヌという表記も見かけます。
Tag:三角形の五心に関する定理まとめ











