曲線の長さを計算する積分公式(弧長積分)
曲線の長さを求める積分公式(弧長積分)について解説します。普通の関数,媒介変数表示,極座標の3つの公式を紹介します。
関数 y=f(x) の曲線の長さ
関数 y=f(x) の曲線の長さ
で表される曲線の の部分の長さは, (ただし, は微分可能で は連続とする)
で表される曲線の の部分の長さ を求めよ。
より,曲線の長さを求める公式を使うと,
例題1の曲線はカテナリー(双曲線関数)と呼ばれる有名な曲線です。 →双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ
→高校数学の問題集 ~最短で得点力を上げるために~のT38では,この問題の別解と計算ミスを減らすために「答えを見積もる方法」も紹介しています。
媒介変数表示された曲線の長さ
媒介変数表示された曲線の長さ
媒介変数表示された曲線の長さは,以下の積分で計算できます。
と媒介変数表示された曲線の の部分の長さは, (ただし, と は微分可能で, は連続とする)
で表される曲線の 部分の長さ を求めよ。
半径1の円なので,周の長さ になるはず。これを公式
を使って計算してみる。 なので,
となる。
で表される曲線の の部分の長さ を求めよ。
, なので,長さ は,
例題3の曲線は等角螺旋と呼ばれる有名な曲線です。 →媒介変数表示された有名な曲線7つ
極座標における曲線の長さ
極座標における曲線の長さ
極座標平面において と表される曲線の の部分の長さは, (ただし, は微分可能で, は連続とする)
この公式を使うと,例えばカージオイド曲線 の長さが, になることがわかります。 →カージオイド曲線のグラフ,面積,長さ
弧長積分の公式について
弧長積分の公式について
- 曲線の長さを求める積分公式を3つ紹介しました。これらの公式は「弧長積分」と呼ばれることがあります。「弧長積分」は曲線の長さ(弧長)を求める積分公式というくらいの意味で,きちんとした数学用語ではありません。
- ルートの中に二乗の和が登場してしまうので,実際積分計算ができるような関数は少ないです。放物線 の長さを求めるのも簡単ではありません( の積分計算をする必要がある)。
弧長積分の公式の導出
弧長積分の公式の導出
まずは媒介変数版の弧長積分を導出します。媒介変数版が証明できたら残りの2つは一瞬です。
曲線を折れ線で近似します。折れ線の数を増やして近似の精度を上げた極限を取ると公式が導出できます。
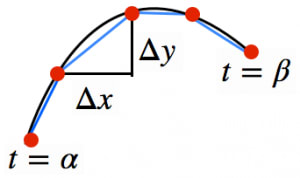
媒介変数が から に変化するとき, の増加量を , の増加量を とおく。
その部分の曲線の長さは,線分の長さで近似できる:
よって,曲線の長さ は折れ線で近似できる:
ここで, の極限を取ったものが曲線の長さである。右辺は微分の定義よりルートの中身 となり,さらに積分の定義より となる。
と媒介変数表示された曲線に媒介変数表示版の公式を適用すると,普通の関数版の公式 が得られる。
と媒介変数表示された曲線に媒介変数表示版の公式を使う。
積の微分公式 → 連鎖律(多変数関数の合成関数の微分) より, となるので,微分の二乗和は となる。つまり,曲線の長さは となる。
さらに に置換すると
という式も得られる。
※上記では「折れ線の長さの和の極限」が曲線の長さに一致すると考えました。実は,この議論は定理の証明というよりも定義と言った方が良いです。つまり,そもそも曲線の長さが「折れ線の長さの和の極限」で定義されます。
定理の前提条件について(気になる人のみどうぞ)
媒介変数版の証明の最後で極限を取るときに,ルートの中身の極限を取ってから全体の極限を取りました。このように一部分だけ先に極限を取る操作は一般には許されません。例えば ですが,左辺を計算するときに分子だけ先に極限を取ると, となります。
しかし,先に極限を取った部分が有限確定値に収束するならこのような操作が可能です。今回の場合は や が微分可能という条件があるのでOKです。
また, や が連続であるので,シグマの極限を取って積分にすることができました(不連続関数に対しては積分は定義できないことがある)。
高校時代,放物線の長さを計算しようとして「計算しんどい」と思った記憶があります。











