ヒポクラテスの定理とその証明
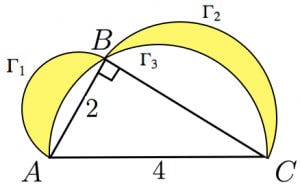
図の黄色部分の面積をできるだけ短時間で求めよ。
ただし, はそれぞれ を直径とする半円です。
ヒポクラテスの三日月と呼ばれる有名問題です(面積を求める図形が三日月っぽい)。中学入試で出そうです。
素直な解法
素直な解法
地道に計算してみましょう。
3つの半円の面積を とおくと求める面積は,
(三角形 の面積)
である,また,三平方の定理より なので
よって答えは,
なんと答えに円周率 は入っていません!
これは になってくれたおかげです。実はこれは偶然ではありません。
ヒポクラテスの定理
ヒポクラテスの定理
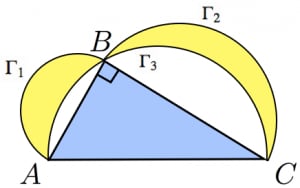
図において,黄色部分の面積と青い部分の面積は等しい。
証明の方針:「相似な図形の面積は対応する部分の長さの二乗に比例する」という重要な事実と三平方の定理から が分かります。
さきほどの解答と全く同様に
黄= 青
なので が成立することを証明すればOK。
これは直角三角形 において三平方の定理が成立することから分かる:
(半円の面積は直径の二乗に比例する)
ヒポクラテスの三日月の美しい性質の背後には三平方の定理があったのです!
ヒポクラテスの定理の応用版
 なお,直角二等辺三角形にヒポクラテスの定理を適用して図形を半分隠してやることで,この図でも黄=青が成立することが分かります。この形も有名です。
なお,直角二等辺三角形にヒポクラテスの定理を適用して図形を半分隠してやることで,この図でも黄=青が成立することが分かります。この形も有名です。
※三日月の境界は を直径とする半円と を半径とする円の弧です。
簡単過ぎじゃないか!って思った人ごめんなさい。











