三角形の五心の覚えておくべき性質を整理
三角形の五心の定義と重要な性質をまとめました。三角形の五心にはおもしろい性質がたくさんあり,大学入試や数学オリンピックで頻出です。
- 初等幾何的性質(図形的な性質)
- 解析幾何的性質(座標やベクトルに関する性質)
をそれぞれ紹介します。
重心
重心

3本の中線(頂点と向かい合う辺の中点を結んだ線)は1点で交わる。この点を重心と呼ぶ。
- 重心は各中線を に内分する。
- 各頂点の平均として表される。
- ベクトルでは,
- 座標平面では,
注:記号について
この記事では三角形 ABC について
- :辺BCの長さ
- :辺CAの長さ
- :辺ABの長さ
- :点Aの位置ベクトル
- :点Bの位置ベクトル
- :点Cの位置ベクトル
を表すことにします。
外心
外心
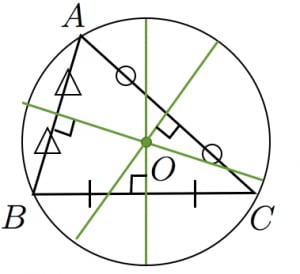
各辺の垂直二等分線は1点で交わる。この点を外心と呼ぶ。
- 外心は三角形 の外接円の中心
- 円周角と中心角の関係:
- 外接円の半径 は,正弦定理: を使って計算できる。
- 外心の位置ベクトル は各頂点の位置ベクトルを用いて以下のように表される: ちなみにこの公式はベクトルの面積比の公式からすぐに導ける。
内心
内心

各角の2等分線は1点で交わる。この点を内心と呼ぶ。
- から各辺までの距離は等しい
- 内心は三角形 の内接円の中心
- 内接円の半径 は,面積 を用いた関係式: を使って計算できる。→内接円の半径と三角形の面積
- 内心の位置ベクトル は各頂点の位置ベクトルを用いて以下のように表される: この公式も外心の場合と同様に面積比を利用して導ける。
垂心
垂心
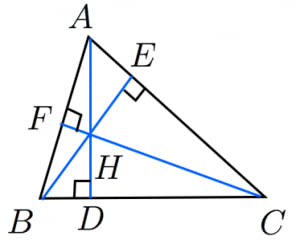
各頂点から向かい合う辺におろした垂線は1点で交わる。この点を垂心と呼ぶ。
垂心の存在については,垂心の存在の3通りの証明参照。
- 四角形 は円に内接する四角形である(円周角の定理や正弦定理が使える)
ちなみに2つめの性質は以下のようにして証明できる:
- 垂心の位置ベクトル も外心,内心と同様の手法で各頂点の位置ベクトルを用いて以下のように表される:
傍心
傍心

1つの角の二等分線と残り2つの角の外角の二等分線の交点は1点で交わる。この点を傍心と言う。
- どの角の内角を考えるかによって傍心は3つあります。図では,∠Aの内角の二等分線上にあるものを示しています。
- 傍心は定義が内心と似ているので,多くの場合内心とほぼ同じ手法で扱えます。(→傍心の意味と性質・内心との比較)
- 外心,重心,垂心は座標やベクトルを用いたゴリ押し計算で扱うこともできますが,内心,傍心は角度に関する情報が本質的な役割を果たすので解析的なアプローチはほとんどの場合で通用しません。
例題
例題
三角形 の内心を , 3つの傍心のうち の二等分線の上にあるものを とする。 と の中点を とする。直線 と 直線 の交点を とする。このとき , であった。
以下の問いに答えよ。
(1) , の大きさをそれぞれ求めよ。
(2) を求めよ。
(3) とおく。 は何度か。 を用いて表せ。
(4) を求めよ。
内心と傍心の融合問題です。角度の情報をうまく用いて直角や共円を見つけ出しましょう。
私の中でのイメージカラーは重心が黒,外心が緑,内心が赤,垂心が青,傍心が黄色です。
Tag:三角形の五心に関する定理まとめ











