正規分布の基礎的な知識まとめ
正規分布の基本的な知識を整理しました。
正規分布とは
正規分布とは
正規分布(ガウス分布)とは,図のような左右対称の連続型の確率分布です。正確な定義(確率密度関数)については後述します。
正規分布は最も代表的な分布の一つです。例えば物理などの実験における測定の誤差,テストの点数などは(ほぼ)正規分布に従う(ことが多い)と考えられています。
また,コイン投げのように,反復試行の成功回数が従う確率分布も(反復試行が多いとき,近似的に)正規分布になります。 →二項分布の正規近似(ラプラスの定理)
この記事では,正規分布について,確率密度関数の式の意味や,平均・分散の導出を中心に解説します。
正規分布の確率密度関数
正規分布の確率密度関数
正規分布の確率密度関数について解説します。
前提知識:確率密度関数の意味と具体例
正規分布(ガウス分布)の確率密度関数は,
です。平均は ,分散は です。
- 正規分布の確率密度関数は複雑そうですが,基本形を考えればだいぶ簡単になります。正規分布の中でも平均が ,分散が であるようなものが特に重要で,標準正規分布と呼ばれます。標準正規分布の確率密度関数は, です。だいぶ簡単になりましたね。
 標準正規分布のグラフは図のようになります。例えば 以上 以下となる確率は斜線部分の面積になります。
標準正規分布のグラフは図のようになります。例えば 以上 以下となる確率は斜線部分の面積になります。- なお,指数関数 において が複雑な式のとき書きづらいので と書いています。
補足
- 多変数バージョン:多変量正規分布の確率密度関数の解説
- 標準正規分布の重要性:正規分布の標準化の意味と証明
1シグマ区間
1シグマ区間
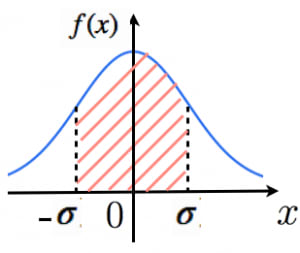
- 正規分布において を「1シグマ(1 )区間」と言います。1シグマ区間に入る確率は約68%です。偏差値40から60に相当します。→偏差値の意味・目安・5つの性質
- 同様に, を「 シグマ区間」と言います。2シグマ区間に入る確率は約95%,3シグマ区間に入る確率は約99.7%です。偏差値20から80の間に約99.7%の人間がいるということになります。
正規分布とガウス積分
正規分布とガウス積分
ガウス積分を用いて三つの重要な性質を証明していきます(→ガウス積分の公式の2通りの証明)。 以下の三つ(正規化・平均・分散)を理解すれば,正規分布 の密度関数がなぜ複雑そうな形をしているのかが分かります。
1(規格化・正規化):正規分布の確率密度関数が本当に確率密度関数であること (全区間で積分すると1となること)を確認します。
ここで, と置換すると,上式は
この積分の部分はガウス積分の公式より
となるので確かに を全区間で積分すると となる。
※積分区間が から なので平行移動しても積分区間は変わりません。
正規分布の平均
正規分布の平均
2(期待値): で表される正規分布の期待値(平均) が であることを証明してみます。これは分布が に関して対称な形をしていることから明らかですが,積分の練習として。
期待値の定義より,
ここで, と置換すると,
第一項の被積分関数は奇関数×偶関数=奇関数なので積分値は ,第二項の積分値はさきほど示したことより なので結局 となる。
正規分布の分散・標準偏差
正規分布の分散・標準偏差
3(分散・標準偏差): で表される正規分布の分散 が であること,つまり標準偏差が であることを証明してみます。
分散の定義より,
ここで, と置換すると
一方,部分積分を使うと,
となるので,ガウス積分の公式より
以上から
正規分布の確率密度関数は 全区間で積分すると1,平均が ,分散が となるようにうまく作られていることが分かりました!
偏差値80を越えるのがいかに難しいことかが分かります。
Tag:数検1級の範囲と必要な公式まとめ











