放物線と直線で囲まれた面積を高速で求める1/6公式

更新 2022/06/23

1/6公式

$\displaystyle\int_{\alpha}^{\beta} (x-\alpha)(x-\beta)dx=-\dfrac{1}{6}(\beta-\alpha)^3$

$\dfrac{1}{6}$ 公式（ろくぶんのいち公式）を使うと，いろいろな面積の計算をすばやくできます。ぜひ覚えておきましょう。

1/6公式を使う例題

1/6公式を使うと，放物線と直線で囲まれた部分の面積をすばやく計算できます。

例題1

$y=x^2$ と $y=x+2$ で囲まれた部分の面積を求めよ。例題1

解答

交点の $x$ 座標を計算すると，
$(x+2)-x^2=0$
$x^2-x-2=0$
$(x+1)(x-2)=0$
$x=-1,2$

よって，求める面積は

$\displaystyle\int_{-1}^2\{(x+2)-x^2\}dx\\ =-\displaystyle\int_{-1}^2(x+1)(x-2)dx$

ここで，1/6公式を使うと上式は $\dfrac{\{2-(-1)\}^3}{6}=\dfrac{9}{2}$

1/6公式 $\displaystyle\int_{\alpha}^{\beta} (x-\alpha)(x-\beta)dx=-\dfrac{1}{6}(\beta-\alpha)^3$

を $\alpha=-1,\beta=2$ として使いました。定積分の計算が一瞬でできています。

放物線と直線で囲まれた部分の面積

例題1と同じように考えると，以下の応用公式が導けます。

応用公式1

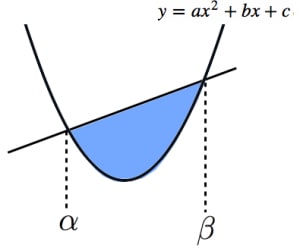
6分の1公式

放物線と直線が2点で交わるとき，その放物線と直線で囲まれた部分の面積は，

$\dfrac{|a|}{6}(\beta-\alpha)^3$

ただし $a$ は放物線の2次の係数
$\alpha,\beta\:(\alpha<\beta)$ は交点の $x$ 座標

面積は，直線の式や2次関数の係数 $b,c$ に直接依存せず $a,\alpha,\beta$ だけで決まります！

$\dfrac{1}{6}$ 公式を使えば簡単に導出できます（ $\dfrac{1}{6}$ 公式自体の証明は後ほど）。

応用公式1の証明

「放物線の式」ー「直線の式」= $a(x-\alpha)(x-\beta)$

と表せるので，放物線と直線で囲まれた部分の面積は， $S=\left|\displaystyle\int_{\alpha}^{\beta}a(x-\alpha)(x-\beta)dx\right|$ と表せる。絶対値の中身の積分は $\dfrac{1}{6}$ 公式より $-\dfrac{a}{6}(\beta-\alpha)^3$ となるので $S=\dfrac{|a|}{6}(\beta-\alpha)^3$

練習問題1

$y=2x^2-7x+7$ と $y=x+1$ で囲まれた部分の面積を計算せよ。

練習問題1の解答

交点の xxx 座標を計算すると，

2x2−7x+7=x+12x^2-7x+7=x+12x2−7x+7=x+1

2x2−8x+6=02x^2-8x+6=02x2−8x+6=0

(x−1)(x−3)=0(x-1)(x-3)=0(x−1)(x−3)=0

x=1,3x=1,3x=1,3
よって，応用公式1より求める面積は
26(3−1)3=83\dfrac{2}{6}(3-1)^3=\dfrac{8}{3}62​(3−1)3=38​

→高校数学の問題集　～最短で得点力を上げるために～のT21では，練習問題1の4通りの解法を紹介しています。

1/6公式の証明

ゴリ押しで普通に定積分を計算することもできますが，計算量を少なくするためのテクニック「 $x-\alpha$ を基準にする」を用います。

証明

$x-\alpha$ を基準にする手法を用いて $x$ ではなく $x-\alpha$ が基準になるように変形して積分を行う：

$\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\ =\displaystyle\int_{\alpha}^{\beta}(x-\alpha)\{(x-\alpha)+(\alpha-\beta)\}dx\\ =\displaystyle\int_{\alpha}^{\beta}\{(x-\alpha)^2+(\alpha-\beta)(x-\alpha)\}dx\\ =\left[\dfrac{(x-\alpha)^3}{3}-(\beta-\alpha)\dfrac{(x-\alpha)^2}{2}\right]_{\alpha}^{\beta}\\ =-\dfrac{(\beta-\alpha)^3}{6}$

となり，求める公式を得る。

被積分関数は因数分解されており， $(x-\alpha)$ という塊を持っているので，わざわざ展開して積分するのではなく， $(x-\alpha)$ を基準に考えることで計算量を減らすことができています。また，この場合は積分区間の下端が $\alpha$ なので $x-\alpha$ を基準にするテクニックの威力が倍増しています（積分された関数に $x=\alpha$ を代入すると0になるので面倒な計算が不要）。

放物線と放物線で囲まれた部分の面積

$\dfrac{1}{6}$ 公式の2つめの応用です。

応用公式2

放物線 $y=a_1x^2+b_1x+c_1$ と， $y=a_2x^2+b_2x+c_2$ の交点の $x$ 座標を $\alpha, \beta\:(\alpha < \beta)$ とおくとき，

2つの放物線で囲まれた部分の面積は，

$\dfrac{\left|a_1-a_2\right|}{6}(\beta-\alpha)^3$

さきほどと同じく面積は2次の係数と交点の $x$ 座標だけで決まることがわかります。この公式も使う機会が多いです。「放物線と直線」の場合とほぼ同様に証明できます。

1/6公式に関連する公式

$\dfrac{1}{6}$ 公式を一般化した定積分の公式として，以下のベータ関数の積分公式があります。 $\displaystyle\int_{\alpha}^{\beta} (x-\alpha)^m(\beta-x)^ndx=\dfrac{m!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
面積を高速に求めるための定積分の公式として， $\dfrac{1}{3}$ 公式や $\dfrac{1}{12}$ 公式というものもあります。→1/3公式と1/12公式の意味と証明【二次関数・三次関数と面積】
これらの公式の理解においては， $\dfrac{1}{6}$ 公式の証明で見たような「定積分における $x-\alpha$ を基準にする考え方」が重要です。多項式で表される曲線同士で囲まれた部分の面積を求める問題は， $x-\alpha$ を基準にする考え方を使うことで計算が楽になると意識しておきましょう。これを応用すれば3次関数と直線で囲まれた部分の面積や3次関数と放物線で囲まれた部分の面積を求める計算量も大きく減らせます。

めんどうな積分計算ほど計算ミスしやすい分野はありません。

Tag:積分を用いた面積，体積の求積公式まとめ

Tag:大学入試共通テストにも役立つ即効性の高い公式まとめ

Tag:積分公式一覧

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！