三角形の五心と頂点までの距離
三角形の五心から各頂点までの距離を素早く導出できるようになっておきましょう!
五心と頂点の距離
五心と頂点の距離
数学オリンピックの図形問題を解くときに,全ての長さや角度を三角形 の長さ と角 で表すことで解く方法があります。予選問題の求値問題にも,本選の証明問題にも使えます。
この手法がうまくいく問題は暗記と機械的な計算だけで解けてしまいます!
そのために暗記すべき重要な公式(手順)として 「三角形の各頂点と五心までの距離」および「三角形の五心間の距離」があります。
この記事では「三角形と各頂点と五心までの距離」の方を扱います。
三角形の外心と頂点の距離
三角形の外心と頂点の距離
簡単な順に紹介します。まずは外心 から。これは正弦定理を使うだけです。
三角形の重心と頂点の距離
三角形の重心と頂点の距離
三角形の垂心と頂点の距離
三角形の垂心と頂点の距離
次は垂心 です。簡潔で美しいので一番使う機会が多いです。

が鋭角の場合で証明する(鈍角の場合もほとんど同様)。
と の交点を とおくと,
以上より,
三角形の内心と頂点の距離
三角形の内心と頂点の距離
内心 と傍心はけっこう大変です。まずは角度を使った綺麗なバージョン。
次は長さのみで表すバージョン。
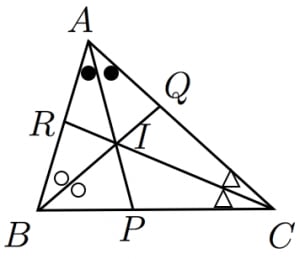
と の交点を とおく。 幾何不等式の練習でも紹介したように,角の二等分線公式を二回使うと, より
が分かる。
ここで,角の二等分線に関する重要な3つの公式の公式3より
これを上式に代入して整理すると公式を得る。
三角形の傍心と頂点の距離
三角形の傍心と頂点の距離
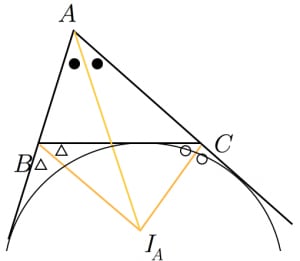
次は傍心 です。ほとんど使う機会はありませんが内心との対応が美しいです。
傍心の意味と性質・内心との比較でも解説したように内心でできることは傍心でもできます。そのため導出方法もほとんど同じです。練習問題にどうぞ!
「三角形 の情報をもとに五心までの距離,五心どうしの間の距離を求めることができる」という知識はいろいろな場面で活躍します。上記の公式たちを覚えるか,必要なときに素早く導出できるようになっておきましょう。
円が登場しない数学オリンピックの図形問題は計算だけで解けるようになりたいというのが自分の願望です。
Tag:三角形の五心に関する定理まとめ












