cosxの微分公式のいろいろな証明
の導関数は,
の微分公式をいろいろな方法で証明します。
コサインの微分のいろいろな証明方法
コサインの微分のいろいろな証明方法
いろいろな方法があります!
1.加法定理で計算(重要)
2.和積公式で計算
3.図形的に解釈
4.平行移動したら になる(重要)
5. を用いる
6. を用いる
1〜3はコサインの微分を直接求める方法です。サインの場合と全く同様(→sinxの微分公式の3通りの証明)です。
4〜6は サインの微分公式: を前提としてコサインの微分を証明します。以下でそれぞれ解説します。
1.加法定理で計算
1.加法定理で計算
なお,最後の極限計算はサインの微分を証明するときと全く同じです。よく分からない方は上記リンク先を参照して下さい。
2.和積公式で計算
2.和積公式で計算
和積公式を用いる証明もサインの微分のときと同様にしましょう。
3.図形的に解釈する
3.図形的に解釈する
こちらもサインのときと同様です。三角関数を微分すると位相が90度進むことが図形的に納得できます。
とおく。
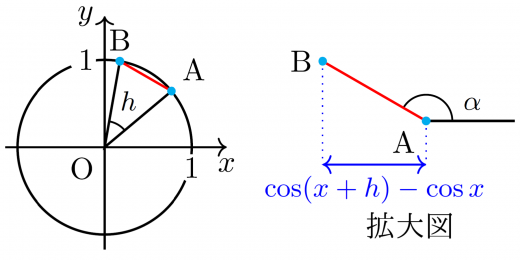
上図から を得る。
三角形 に余弦定理を用いることで を得る。こうして が によって表された。
また, が に近いとき, は における単位円の接線に近づくので, を得る。
よって, を得る。
4.平行移動を用いる
4.平行移動を用いる
5.三角関数の公式を用いる
5.三角関数の公式を用いる
以下二つの証明は邪道ですが,面白いので解説します。
こうした計算方法は逆関数の導関数の計算などに利用できるため,覚えておいて損はないです。
を用いて証明します。なお, が連続微分可能であることを仮定しています。
の両辺を で微分する(合成関数の微分公式を用いる)と,
よって, なる では である。
導関数が連続関数という仮定のもと, なる点でも が成立する。
6.倍角の公式を用いる
6.倍角の公式を用いる
5と似たような方法ですが,今回はサインの倍角公式を用います。同様に が連続微分可能であることを仮定しています。
の両辺を微分すると,
ただし,左辺では合成関数の微分,右辺では積の微分公式を用いた。両辺を2で割り,倍角の公式を用いると,
整理すると,
となる。
よって, なる では
導関数が連続関数という仮定のもと, なる点でも が成立する。
証明5,地味に好きです。
Tag:微分公式一覧(基礎から発展まで)











