ヴァンデルモンドの畳み込みの3通りの証明
任意の非負整数 に対して,
という恒等式が成立する。これをヴァンデルモンドの畳み込みと言う。 ただし, のとき と定義する。
ヴァンデルモンドの畳み込みについて
ヴァンデルモンドの畳み込みについて
- ヴァンデルモンドの畳み込み(Vandermonde’s convolution),ヴァンデルモンドの恒等式(Vandermonde’s identity)などと呼ばれる有名な式です。
例えば, としてみると,
- 左辺は
- 右辺は
となり確かに等しい。
-
としてみると, となります。さらに を使うと, となります。これは,二項係数の和,二乗和,三乗和でも紹介した有名な式です。
-
以下では,ヴァンデルモンドの畳み込みを3通りの方法で証明します! 二項係数の関係式を導く良い例題です。
二項定理を用いた証明
二項定理を用いた証明
二項係数の関係式を証明する問題の多くは,二項定理をうまく利用すると解けます。式の形を見てうまく適用する必要があるので,鍛錬と少しの発想力が必要です。
ヴァンデルモンドの畳み込みの右辺 は を展開したときの の係数である。
この係数をもう1つ別の方法で求める。
の係数は となる に対応する項から出てくるので以下のように表される:
これは,ヴァンデルモンドの畳み込みの左辺なので,証明完了。
場合の数を2通りの方法で考える証明
場合の数を2通りの方法で考える証明
以下のような証明方法もあります。
男 人,女 人,合計 人の中から 人選ぶ場合の数を考える。
-
全体 人から一挙に 人選ぶと 通りで, 右辺の式になる。
-
男を何人選ぶかで場合分けして足し上げると左辺の式になる。具体的には,男が 人で女が 人,を まで足し上げると
さらに,ここでは省略しますが最短経路の数に意味づけて証明することもできます。
二項係数の関係式を証明するテクニックに関しては二項係数の有名公式一覧と2つの証明方針も参考にしてみてください。
数学的帰納法を用いた証明
数学的帰納法を用いた証明
二項係数の関係式を証明する問題の多くは,数学的帰納法を用いれば大抵クリアできます。パスカルの三角形の性質を用います。
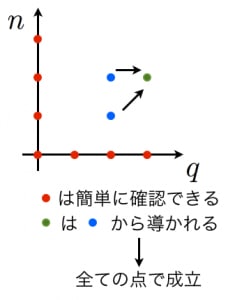
に関する数学的帰納法で証明する。 のときは より成立。
のときは,左辺も右辺も となり成立。
および で成立すると仮定して の場合を考える。
ここで,1行目から2行目への変形と,最終行への変形で二項係数の関係式(パスカルの三角形の性質)を用いた。3行目から4行目への変形で帰納法の仮定を用いた。
このように, パスカルの三角形の性質を用いて の小さい場合に帰着させて帰納法で証明する手法は頻出なのでおさえておきましょう!
なお,2014千葉大後期数学科で,ヴァンデルモンドの畳み込みと似たような問題が出題されたらしいです。
二項係数の関係式は代数的にも証明できるし場合の数の意味を考えても証明できることが多い,いろいろな方法を試してみよう。











