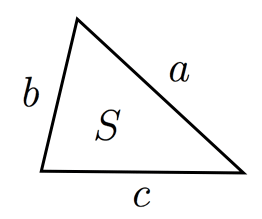平面図形
更新
外接円の半径と三角形の面積の関係(S=abc/4R)
外接円の半径と三角形の面積の関係(S=abc/4R)
三辺の長さが の三角形の外接円の半径を , 面積を とおくとき以下の美しい関係が成立する。
検算に使える公式なので,受験生は覚えておくとよいでしょう。
ヘロンの公式の証明と使用例
ヘロンの公式の証明と使用例
オイラーの定理(内心と外心の距離)とオイラーの不等式の証明を3通りずつ
オイラーの定理(内心と外心の距離)とオイラーの不等式の証明を3通りずつ
内心と外心の距離を求める公式です。
内接円の半径を ,外接円の半径を とおくとき,外心 と内心 との距離 は以下の式で表される:
非常に美しい定理です。
トレミーの定理とその3通りの証明,応用例
トレミーの定理とその3通りの証明,応用例
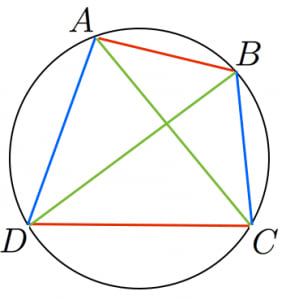
ブラーマグプタの公式とその2通りの証明
ブラーマグプタの公式とその2通りの証明
ブラーマグプタの公式:
円に内接する四角形 において とおくと,四角形 の面積は,
ただし, とおいた。
ブレートシュナイダーの公式
ブレートシュナイダーの公式
一般的な四角形の面積を求める公式(ブラーマグプタの公式の一般化)。
ブレートシュナイダーの公式:
四角形 において, , とおくと,
四角形の の面積 は,
ただし, とおいた。
四角形が円に内接する場合 より,ブレートシュナイダーの公式はブラーマグプタの公式と一致します。
三角形の五心の覚えておくべき性質を整理
三角形の五心の覚えておくべき性質を整理
三角形の五心は有名ですが非常に豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出です。三角形の五心の定義と重要な性質をまとめておきます。
傍心の意味と性質・内心との比較
傍心の意味と性質・内心との比較
傍心に関する性質は内心に関する性質とほとんど同じ。
傍心,傍接円に関して迷ったらまずは内心,内接円を考えるとよい。
三角形のフェルマー点の3通りの証明
三角形のフェルマー点の3通りの証明
最大角が 未満の三角形 においてはフェルマー点は三角形の内部に存在して,
三角形の面積比にまつわる公式たち
三角形の面積比にまつわる公式たち
三角形の面積比,四面体の体積比にまつわる重要な公式を3つ紹介します。
フランク・モーリーの定理の証明
フランク・モーリーの定理の証明
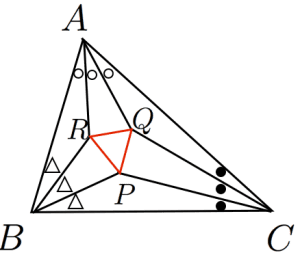
フランクモーリーの定理:
任意の三角形 に対して,3つの角の三等分線どうしが最初にぶつかる点を とおくとき三角形 は正三角形である。
角の二等分線に関する重要な3つの公式
角の二等分線に関する重要な3つの公式
中線定理の3通りの証明
中線定理の3通りの証明

中線定理(パップスの中線定理)とは,図において
が成立するという定理。ただし, は の中点。
チェバの定理:例題と3通りの証明
チェバの定理:例題と3通りの証明

チェバの定理:
図において,
が成立する。これをチェバの定理と言う。
スチュワートの定理の証明とその仲間
スチュワートの定理の証明とその仲間

スチュワートの定理:
三角形 と辺 上の点 に対して,
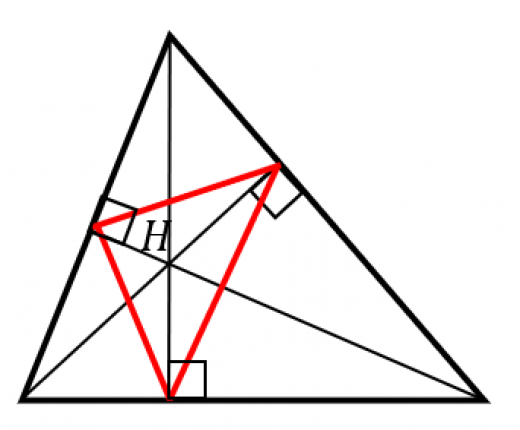
九点円の定理の証明と諸性質
九点円の定理の証明と諸性質

九点円の定理:
三角形 において,以下の9点は同一円周上にある。
三辺の中点
垂線の足
垂心と各頂点の中点
シュタイナーレームスの定理
シュタイナーレームスの定理

シュタイナーレームス(Steiner-Lehmus)の定理:
三角形 において の二等分線と の交点を , の二等分線と の交点を とおく。
ならば
根軸の性質と根心の存在定理
根軸の性質と根心の存在定理
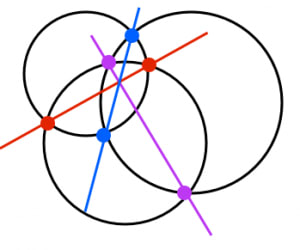
根心の存在定理:
3つの円が互いに2点で交わるとき,三本の根軸は一点で交わる。
2つの円が2点で交わるとき,その2点を結んだ線を根軸(radical axis)と言います。
三角形の決定条件と自由度
三角形の決定条件と自由度
三角形の自由度は である。すなわち,三角形に関して(独立な)3個の情報が与えられたら残りの情報も分かる
接する2つの円の相似の中心
接する2つの円の相似の中心
ケージーの定理とその証明
ケージーの定理とその証明

ケージーの定理(Casey’s Theorem):
互いに交わらない4つの円 がそれぞれ点 で別の円 に(この順番に)内接しているとき,円 と の共通外接線の長さを とおくと,
2つの円の位置関係
2つの円の位置関係
2つの円の位置関係は5通りあり,中心間の距離と半径によって状況が変わってくるのでどのパターンなのか把握することが重要です。このページでは5通りの分類,交点,接線,相似の中心について整理します。
垂心の存在の3通りの証明
垂心の存在の3通りの証明

三角形 において各頂点から向かいの辺に下ろした3本の垂線は一点で交わる。その点を垂心と呼ぶ。
線分の長さにまつわる頻出の形
線分の長さにまつわる頻出の形
図形問題における頻出の構図を2つ紹介します。いずれも線分の長さを最小化する問題です。
内接円に関する数オリ頻出の図形
内接円に関する数オリ頻出の図形

定理:三角形 の内接円と辺 の接点を とおく。 から辺 と垂直な直線と内接円の交点を とおく。さらに と の交点を とおくとき,
正方形の頂点と最短距離
正方形の頂点と最短距離
2014年IMO第4問の解説
2014年IMO第4問の解説
今年の数学オリンピックの問題です:
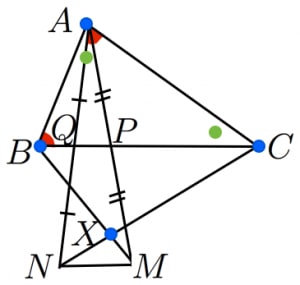
鋭角三角形 の辺 上に
となるように取る。また, の中点が , の中点が となるように を取る。
このとき と の交点 が の外接円上にあることを証明せよ。
アポロニウスの円の証明と応用
アポロニウスの円の証明と応用
アポロニウスの円がなぜ嬉しいのか?
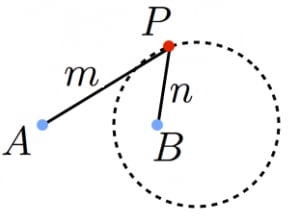
アポロニウスの定理:
2点 からの距離の比が で一定である点の軌跡は円である。これをアポロニウスの円と呼ぶ。
なお, のときの軌跡は の垂直二等分線になりますが,これを半径無限大の円とみなすとアポロニウスの定理は崩れません。
図形の美しい3つの定理〜逆数の和〜
図形の美しい3つの定理〜逆数の和〜
逆数の和に関する平面図形の美しい定理を3つ紹介します。実用的な定理ではありませんが,証明はよい練習問題になるのでトライしてみてください!
円に外接する四角形とその性質
円に外接する四角形とその性質
円に外接する四角形 において,
方べきの定理の意味と2通りの証明
方べきの定理の意味と2通りの証明

方べきの定理とは,円と点 と2本の直線が作る図形において,
が成立するという定理です。方べきの定理は全部で3パターンあります。
この記事では, 方べきの定理の意味と証明 を3パターンそれぞれ解説します。最後に,3つのタイプを統一的に証明する方法を解説します。
三角形の五心と頂点までの距離
三角形の五心と頂点までの距離
三角形の五心と各頂点までの距離は素早く導出できるようになっておきましょう!
三角形の成立条件とその証明
三角形の成立条件とその証明
複比の定義と複比が不変であることの証明
複比の定義と複比が不変であることの証明
複比(Cross-ratio):
同一直線上の四点 に対して複比を,
と定義する。
図形問題への応用を念頭に置いているので厳密さよりもわかりやすさを重視しています。
調和点列の様々な定義と具体例
調和点列の様々な定義と具体例
調和点列:
同一直線上に四点 がこの順にあるとき,
1: (線分 を同じ比で内分する点 と外分する点 )
ならば四点 を調和点列と言う。
第一余弦定理とその3通りの証明
第一余弦定理とその3通りの証明
ニュートンの定理とその証明
ニュートンの定理とその証明
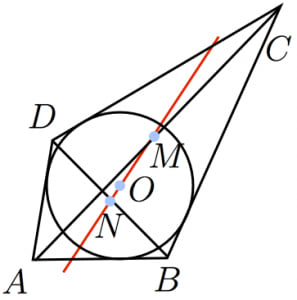
ニュートンの定理:
中心が である円に外接する四角形 において対角線 と の中点をそれぞれ とおくと, は同一直線上にある。この直線をニュートン線と呼ぶ。
反転幾何の基礎
反転幾何の基礎
反転変換:
中心 ,半径 の円 がある。このとき,円 による反転を以下のように定義する。
の行き先は,半直線 上の点で, を満たす点
数学オリンピックでたまに使える「反転」という手法についての基礎的な事柄を解説します。
デザルグの定理とその三通りの証明
デザルグの定理とその三通りの証明

デザルグの定理:
三角形 と がある。このとき,
, , が一点 で交わる
→ と の交点 , と の交点 , と の交点 は同一直線上にある。
メネラウスの定理の覚え方と拡張
メネラウスの定理の覚え方と拡張
等角共役点とその証明
等角共役点とその証明

等角共役点:三角形 と点 がある。
角の頂点を通る直線 と角の二等分線に関して対称な直線 を の等角共役線という。
の等角共役線は一点で交わり,これを の等角共役点という。
平面図形の非常に美しい定理です。
ジュルゴンヌ点とナーゲル点の存在証明
ジュルゴンヌ点とナーゲル点の存在証明
ジュルゴンヌ点(Gergonne point):

三角形 において内接円と各辺の接点を とおくとき, は一点で交わる。この点をジュルゴンヌ点という。
ヒポクラテスの定理とその証明
ヒポクラテスの定理とその証明
三平方の定理の4通りの美しい証明
三平方の定理の4通りの美しい証明
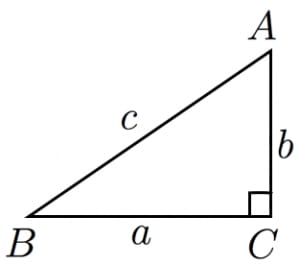
三平方の定理(ピタゴラスの定理): であるような直角三角形において,
円に内接する四角形の性質とその証明まとめ
円に内接する四角形の性質とその証明まとめ
円に内接する四角形の性質を整理しました。円周角の定理からトレミーの定理まで,全部使えるようになっておきましょう!
正五角形の対角線の長さと作図方法
正五角形の対角線の長さと作図方法
正五角形を(定規とコンパスのみを使って)作図する方法を解説します。
正五角形の作図の原理を理解するために,まずは1辺が1の正五角形の対角線の長さについて考えます。とにかく作図方法だけ知りたい!という方はページ下部のグレー背景部分(2箇所)のみ読んで下さい。
全ての三角形が二等辺三角形であることの証明!?
全ての三角形が二等辺三角形であることの証明!?
有名な嘘の証明です。
全ての三角形が二等辺三角形であること,さらに正三角形であることの証明を解説します。もちろんそのような命題が成立するはずはないので証明のどこかに嘘があります。探してみてください!
ルーローの三角形と定幅図形
ルーローの三角形と定幅図形
ルーローの三角形と定幅曲線について。意味や応用などを解説します。
東大数学(図形問題)のポイントと例題
東大数学(図形問題)のポイントと例題
- 難関大の図形問題は「どの道具を使って解答するか」から考える必要があることも。
- 昔の東大入試では簡単な問題も出題されている。
東大の問題とその解説を通じて「図形問題における道具選び」について考えます。
Kiepertの定理とその証明
Kiepertの定理とその証明

Kiepert(キエペルト,キーペルト)の定理:
三角形 の外側(または内側)に相似な二等辺三角形 をつくる。このとき, は一点 で交わる。
垂心,フェルマー点,ナポレオン点などを包含している非常に美しい定理です。
円に内接する三角形の面積の最大値
円に内接する三角形の面積の最大値
射影平面の3通りの定義
射影平面の3通りの定義
射影平面とは
1.いつもの平面に無限遠点を加えたもの
2.半球を貼りあわせたもの
3.三次元空間中の原点を通る直線の集合
内接円の半径と三角形の面積
内接円の半径と三角形の面積
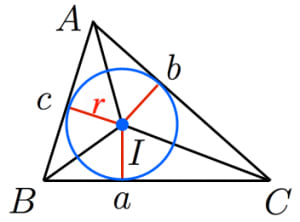
内接円とは,三角形の3つの辺全てに接する円のこと。内接円の半径は,
という公式を使って計算することができる。
三角形の内接円について詳しく解説します。前半では,内接円の半径の計算公式の意味を解説し,後半では公式を2通りの方法で証明します。
円周率の求め方(いろいろな計算式)
円周率の求め方(いろいろな計算式)
円周率の近似値の求め方をいろいろ紹介します。実際に計算して収束の速さについても見てみます。
接弦定理の意味・例題・証明・逆をわかりやすく
接弦定理の意味・例題・証明・逆をわかりやすく
相似比と面積比・体積比:いろいろな例と証明
相似比と面積比・体積比:いろいろな例と証明
相似な平面図形について,面積比=相似比の二乗
相似な空間図形について,体積比=相似比の三乗
面積比をきちんと理解できれば体積比もほぼ同様に理解できるので「面積比=相似比の二乗」を中心に解説します。
平方根の長さを作図する2通りの方法
平方根の長さを作図する2通りの方法
任意の正の有理数 に対して,長さ の線分が与えられれば長さ の線分を定規とコンパスで作図できる。
長さ の線分を作図できるということは,面積 の正方形を作図できるということでもあります!
sinを用いた三角形の面積公式
sinを用いた三角形の面積公式
ルモアーヌ点(類似重心)とその性質
ルモアーヌ点(類似重心)とその性質

三角形 において,「中線を角の二等分線に関して折り返した直線」は 本あるが,それらは 点で交わる。
この点をルモアーヌ点(類似重心,Symmedian Point,Lemoine Point)と言う。
三角形の中心(36個)を図示してみた
三角形の中心(36個)を図示してみた
三角形の中心としては,五心(外心,内心,重心,垂心,傍心)が有名ですが,実は他にもたくさんあります。
ミケルの定理とミケル円
ミケルの定理とミケル円

ミケルの定理:
3点 と直線 上の点 , 上の点 , 上の点 がある。この6点は全て異なるとする。
このとき,三つの円 , , は一点で交わる。
平面幾何の美しい定理4つ
平面幾何の美しい定理4つ
平面図形の美しい定理を4つ紹介します。
四角形の重心の2通りの求め方と注意点
四角形の重心の2通りの求め方と注意点
三角形の重心は高校数学で習いますが,四角形については習いません。というわけで,四角形の重心について考えます。
等周問題に関連する高校数学の問題
等周問題に関連する高校数学の問題
周の長さが一定である図形の中で,面積が最大のものは円です。(等周定理)
等周定理の厳密な証明は少し大変なので,ここでは等周定理に関連して「対称性が高い図形は面積が大きい」というテーマで,高校数学で分かる性質をいくつか紹介します。
図形の対称移動・グラフの対称移動
図形の対称移動・グラフの対称移動
ある図形を,ある直線に関して折り返す移動を線対称移動という。
ある図形を,ある点を中心に 回転させる移動を点対称移動という。
この記事では,図形やグラフの移動の代表例である 線対称移動,点対称移動 について解説します。
円の方程式と関連問題|座標・ベクトル・複素数
円の方程式と関連問題|座標・ベクトル・複素数
平面,空間上の2点間の距離について
平面,空間上の2点間の距離について
平面内の2点 の間の距離 は で与えられる。
また,空間内の2点 の間の距離 は で与えられる。
平面あるいは空間内にある2点間の距離を,点の座標によって表す数式です。
リサージュ曲線の定義とそれに関連する話
リサージュ曲線の定義とそれに関連する話
媒介変数表示
媒介変数表示
媒介変数表示とは,「関連する変数同士の関係を他の変数を用いて表すこと」です。
変数同士を繋ぎ,関係を作っている変数を,媒介変数またはパラメータと呼びます。媒介変数としては などがよく使われます。
媒介変数表示をパラメータ表示と呼ぶこともあります。
この例では,直接 と の関係を表すのでなく, を用いて間接的に関係を表しています。
高校では,媒介変数表示は数学Bのベクトルと数学Ⅲの平面上の曲線で学習します。
直角三角形の定義とさまざまな公式
直角三角形の定義とさまざまな公式
垂足三角形の意味と5つの性質
垂足三角形の意味と5つの性質
円周角の定理とその逆の証明
円周角の定理とその逆の証明
- 中心角は円周角の2倍
- 同じ弧に対する円周角は全て等しい
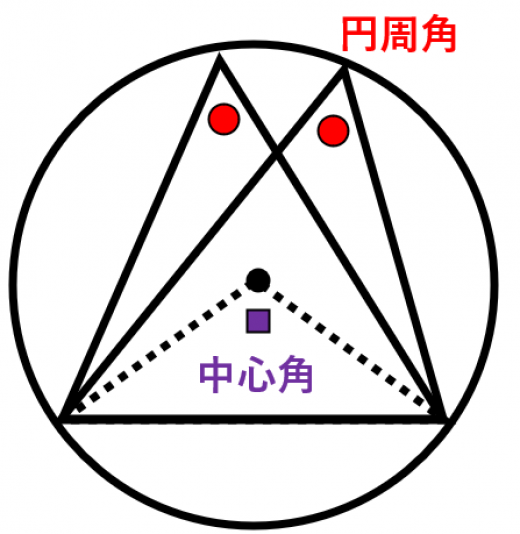
円周角の定理は,中学で習い高校でもよく使う重要な定理です。
この記事では,円周角の定理とその逆について意味と証明を紹介します。
垂直二等分線
垂直二等分線
座標を用いた射影平面の定義
座標を用いた射影平面の定義
に次のように同値関係 を定める。
に対して
ある でない実数 があって,,,
この同値関係による商 を射影平面 という。
この記事では座標を用いた射影平面の定義を紹介します。