球の体積と表面積の公式の覚え方・積分での求め方
半径 の球の表面積は 球の体積は である。
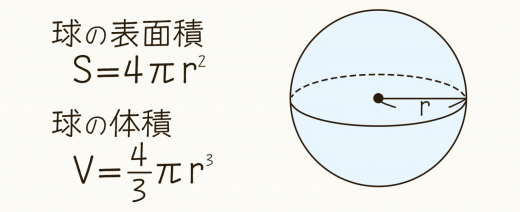
球の体積と表面積の公式の覚え方を紹介します。そのあと,中学生の方向けに公式を利用して例題を解いてみます。後半では積分を使って公式を証明します。表面積は3通りの方法を解説します。 高校生の方にとっては,積分の感覚をつかむよい練習になります。
球の体積と表面積の公式の覚え方
球の体積と表面積の公式の覚え方
以下の語呂合わせで覚える方法が有名です:
- 球の表面積: →「心配アール二乗」
- 球の体積: →「身の上に心配アール三乗」
意味はわからないかもしれませんが,何度も口に出していると自然と覚えます。私も,球体の表面積や体積を求めるときは,今でも語呂で公式を思い出しています。
球の体積と表面積の公式を用いた例題
球の体積と表面積の公式を用いた例題
体積の公式を使う問題
半径 の半球の体積を求めよ。
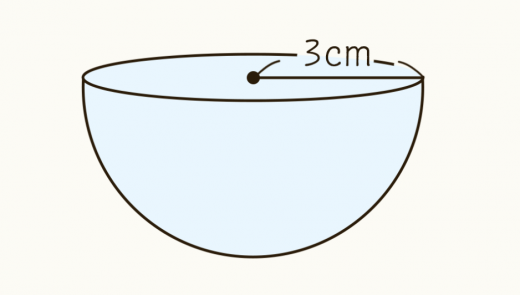
半径 の球の体積 は
半球の体積は,この半分なので,
よって答えは である。
表面積の公式を使う問題
半径 の半球の表面積を求めよ。

半径 の球の表面積 は
半球の表面積は,「この半分」と「半径 の円の面積」を足したものなので,
よって答えは である。
公式の証明の前に
公式の証明の前に
証明の前に,球の表面積と体積に関して意識しておくべきことを整理しました。
- 表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。よって,公式を覚えていなくても ということが分かります。 がだいたい で が より少し大きいというわけです。特に,体積が一辺 の立方体 個ぶんちょっとということは感覚的に納得できます。
- 高校数学では,そもそも曲面の面積ってなんだ?って感じなので,表面積の導出に関しては一部厳密でない表現も含まれています,ご了承ください。
球の体積の求め方
球の体積の求め方
球の体積公式を証明します。数学Ⅲで習う「回転体の体積を求める公式」を使います。球を輪切りにして体積を足しあわせます。
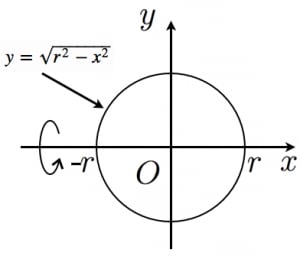
平面上で原点を中心とした半径 の円板 を 軸の回りに回転させた立体は半径 の球である。
の境界の上半分は である。
よって,
球の表面積の求め方1
球の表面積の求め方1
球の表面積を積分で直接求めに行きます。
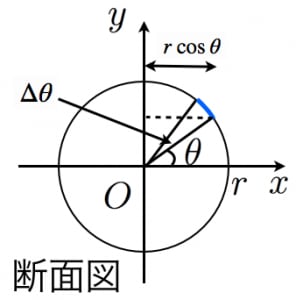
緯度が から の部分(帯のような図形※)の表面積を考える。
周の長さは ,帯の幅は なので帯の表面積は,
よって, の極限を考えることで
※イメージするのが難しい方は,地球儀を持ってきて「緯度が30度から31度の間の部分(帯)」を考えてみてください。帯は十分細いので長方形とみなすと,面積は「帯の長さ」×「帯の幅」で計算できます。帯の長さが になり,帯の幅が になります(帯の幅は,上図の青い線の長さ,つまり「半径が で中心角が であるおうぎ形」の弧の長さです)。
球の表面積の求め方2
球の表面積の求め方2
次に球の体積公式を用いた方法です。
球の体積を で微分したものが球の表面積になることが分かります。
半径 の球の表面積を と書く。半径 の球を「薄い球殻」を寄せ集めたものとみなして体積を求める。
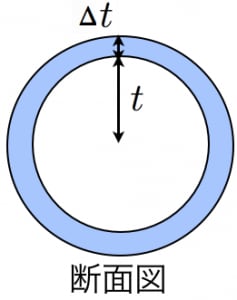
三次元空間において原点からの距離が 以上 以下の間にある部分を考える(このような図形を球殻と呼ぶ)。
が十分小さいとき,この球殻の体積は とみなせる(表面積×厚さ)。このような球殻を から まで寄せ集めたものが半径 の球であり,体積は である。
よって, の極限で
両辺を で微分すると を得る。
球の表面積の求め方3
球の表面積の求め方3
上記の二つの導出方法よりも感覚的な説明になってしまいますが,以下の見方も面白いです。
円の面積や周の長さの公式と同様に重要な公式なので,しっかりと理解しましょう。











