アステロイド曲線の重要な性質まとめ
で表される曲線をアステロイド曲線(星芒形)と呼ぶ。
アステロイド曲線の媒介変数表示
アステロイド曲線の媒介変数表示

-
アステロイド曲線は媒介変数 を用いて と表すことができます。
-
アステロイド曲線は,半径 の円内を半径 の円が滑らずに転がるときの1点(図の青い点)の軌跡として表されます。 サイクロイド曲線の軌跡と同様にして以下のように証明できます。
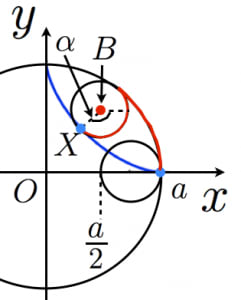
回転したあと円の中心 は となる。
また, と 軸の正の向きがなす角は は,
を満たすので,
よって, の座標は,三倍角の公式を用いることにより
であることが分かり,アステロイドの媒介変数表示と一致する。
アステロイドと線分の通過領域
アステロイドと線分の通過領域
長さ
の線分が移動(両端点はそれぞれ
軸,
軸上を動く)するときの包絡線はアステロイド曲線
になる。
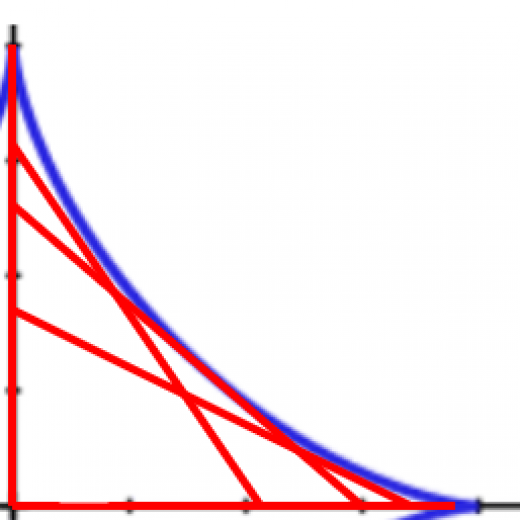
線分の通過領域の境界がアステロイド曲線になります(赤い線分はすべて長さ でアステロイドに接する)。
線分の方程式 において, を固定して が から まで動くときの の最大を求める。微分すると, よって のとき が最大。もとの線分の方程式 に代入すると より
以上2式より を消去すると
アステロイド曲線の面積
アステロイド曲線の面積
「媒介変数表示された曲線で囲まれた部分の面積公式」に従ってひたすら計算します。入試問題としてはややきつめの計算量です。
アステロイド曲線の長さ
アステロイド曲線の長さ
「媒介変数表示された曲線の長さの公式」を用いて計算します(今は学習指導要領の範囲外なので,ほとんどの大学の入試では出題されないと思います)。
面積より計算量は少ないです。
対称性より,第一象限の長さを計算して 倍すればよい。
名前もグラフの概形もかっこいいので,好きな曲線ランキングがあったらNo1でしょう











