スネルの法則(屈折の法則)をフェルマーの原理を用いて証明
フェルマーの原理とスネルの法則ついて紹介します。物理の話題ですが,後半はかなり数学です(座標計算&合成関数の微分)。
スネルの法則
スネルの法則
スネルの法則(屈折の法則)とは,二種類の異なる媒質(例えば水と空気)の境界で光線がどのような振る舞いをするか述べたものです。
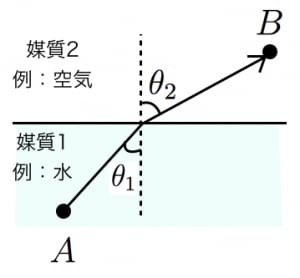
入射角と屈折角のサインの比は媒質中の光の速さの比と等しい:
ただし,媒質1での光の速さを ,媒質2での光の速さを とおきました。
スネルの法則をもっと基本的な原理であるフェルマーの原理を用いて証明(導出)するのが,この記事の目標です。
フェルマーの原理
フェルマーの原理
点 を通った光がどのような経路を通って別の点 までたどりつくのか?その答えがフェルマーの原理です:
光は最短時間で到達できる経路を通る。
- 一様な媒質中では光の進む速さは一定なので「最短時間」を達成する経路と「最短距離」を達成する経路は同じで,それは二点間を結ぶ線分です。
- フェルマーの原理は光学における基本的な原理です。ニュートンの方程式などと同じく証明できるたぐいのものではありません。
- より厳密には変分法を使って定式化されます。上では「最短時間」と述べましたが厳密には時間最小ではなく時間極小となる経路が達成されます。
スネルの法則の導出の概要
スネルの法則の導出の概要
さきほどのスネルの法則の図にフェルマーの原理を適用してみましょう。

光は点 から点 まで最短時間で到達します。
のとき, と を線分で結ぶよりも素早く移動できる媒質2で距離を稼ぎます。
余談ですが,光でなくて人間でも「 から に一刻もはやく行きたい! けど下側の領域にはまんべんなく犬のフンが落ちているので通りたくない!」という場合は図のような経路を通りたくなるでしょう。
さて,途中境界をまたぐ点を とすると 間, 間は線分で移動するのが明らかに最短時間なので,あとは全体の到達時間を最小にする の座標を求めれば光の経路が分かります。ここからは数学の問題です。
具体的な計算
具体的な計算
途中で合成関数の微分を用います。知らない方は合成関数の微分公式と例題7問をどうぞ。難関大の入試に出そうなレベルです。
追記:2004年の九州大学の後期第2問に類題ありです!

を定数として, とおく。 を から の間で動かしたときに最短時間となるようなものを求める。
間の移動にかかる時間は, ,
間の移動にかかる時間は,
これらの和を とおく。 が最小となる を求めるために微分する:
頑張ってもう一度微分すると
よって, は区間内で単調増加。また, で かつ で である。以上より は区間内でただ一つの解 を持つ。
また, で は最小となる。よって実現される経路では の座標は である。
では を満たすので, より
これを変形すると(注),
となる。
注: , です。
フェルマーの原理は光が意思を持っているみたいで面白いですね。











