正弦定理の証明を6つ紹介します。
まずは,正弦定理の簡単バージョン:
sinAa=sinBb=sinCc
の証明を3つ紹介します。
証明1:垂線の長さに注目する方法
証明
鋭角三角形における場合を示す。
C から AB に引いた垂線の足を H とおく。
 sin の定義より,
sin の定義より,
- sinA=bCH
- sinB=aCH
よって,CH を2通りの方法で表すと,bsinA=CH=asinB
両辺を sinAsinB で割ると sinAa=sinBb を得る。
同様に,A から BC に引いた垂線の長さを考えることで,
sinBb=sinCc
も導かれる。
三角形 ABC が直角,鈍角三角形である場合にも,(図は多少変わりますが)ほとんど同じように証明できます。
証明2:余弦定理を用いる方法
sinAa=sinBb=sinCc
を証明します。
余弦定理を用いて変形します(余弦定理について,詳しくは ベクトルの内積を用いた余弦定理の証明 をご覧ください)。
証明
sin2Aa2=1−cos2Aa2=1−(2bcb2+c2−a2)2a2=4b2c2−(b2+c2−a2)24a2b2c2=(a+b+c)(a+b−c)(a−b+c)(−a+b+c)4a2b2c2
これは,a,b,c に関して対称であるので(あるいは同様に計算すると),
sin2Bb2,sin2Cc2
と等しいことがわかる。
証明3 三角形の面積を用いる方法
三角形の面積の公式を認めれば,そこから正弦定理を示すこともできます。
証明
三角形 ABC の面積 S は,
S=21bcsinA=21casinB=21absinC
である。(左辺)=(中辺)より,
sinBb=sinAa
また(中辺)=(右辺)より,
sinCc=sinBb
これより,
sinAa=sinBb=sinCc
を得る。
証明4:円周角を用いる方法
ここからは,sinAa=sinBb=sinCc=2R
を示す証明を3つ与えます。
一つ目は,外接円の半径との関係も含めて証明する方法です。
sinAa=2R を証明します。sinBb=2R,sinCc=2R も全く同様に証明できます。
証明
- A<90∘ の場合
BA′ が外接円の直径となるような A′ を取る。

円周角の定理より,∠BAC=∠BA′C なので,sinA=sinA′=2Ra となる。つまり sinAa=2R
- A=90∘ の場合
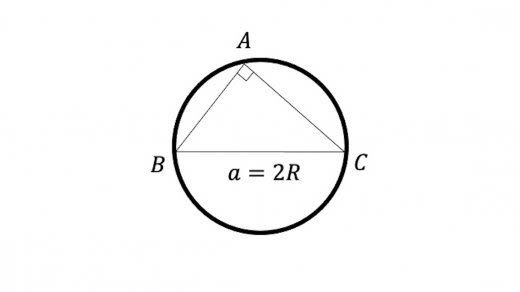
sinA=1 である。また,BC は外接円の直径なので a=2R となる。つまり,sinAa=2R
- A>90∘ の場合

BA′ が外接円の直径となるような A′ を取る。円に内接する四角形の性質より,∠BAC=180∘−∠BA′C なので,sinA=sinA′=2Ra となる。つまり sinAa=2R
証明5:中心角を使う方法
中心角に着目して sinAa=2R を証明します。鋭角三角形の場合のみ証明します。
証明

円周角の定理より,
∠A=21∠BOC=∠MOC
よって,
sinA=sin∠MOC=COMC
ここで,CO=R(外接円の半径),MC=2a
(M
は
BC
の中点)なので,
sinA=2Ra
よって,sinAa=2R
証明6:座標を用いる方法
最後は座標を使って正弦定理を解析的に証明します。このように座標を使うときでも、幾何学的考察は欠かさないようにするのがポイントです。
2通りの座標の取り方を紹介します。
証明
方針1:外接円の中心を原点にとる
∠A が鋭角の場合のみ示す。下図のようにxy座標系を取る。三角形 ABC の外接円の中心が原点である。また,点 B(R,0) としても一般性を失わない。

辺 BC の長さについて,
a2=R2(1−cos2A)2+R2sin22A=R2(2−2cos2A)=2R2(1−cos2A)=4R2sin2A
よって,
sinAa=2R
また,三角形の1点を原点とする座標でも証明できます。
証明2
方針2:三角形の1点を原点にとる
∠A が鋭角の場合のみ示す。下図のように,三角形 ABC の点 A を原点としたxy座標を考える。

三角形 ABC の外接円の中心 O の座標を求める。
線分 AC の傾きは tanA であり,中点 D の座標は (21bcosA,21bsinA) である。
直線 DO は,線分 AC の垂直二等分線であるから,傾きは −tanA1 であり,点 D を通る。ゆえに直線 DO の式は
y=−tanA1(x−21bcosA)+21bsinA
点 O は直線 x=2c 上にあるから,y座標は
y=−tanA1(2c−21bcosA)+21bsinA=−2ctanA1+2btanAcosA+21bsinA=2sinA−ccosA+bcos2A+bsin2A=2sinAb−ccosA
線分 AO の長さは R であるから,
R2=4c2+4sin2A(b−ccosA)2=4sin2Ab2+c2−2bccosA
ここで,余弦定理より
a2=b2+c2−2bccosA
であったから,
R2=4sin2Aa2
ゆえに
sinAa=2R
が得られる。
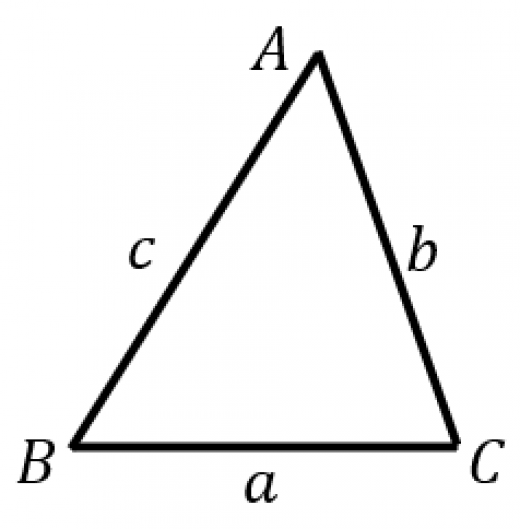
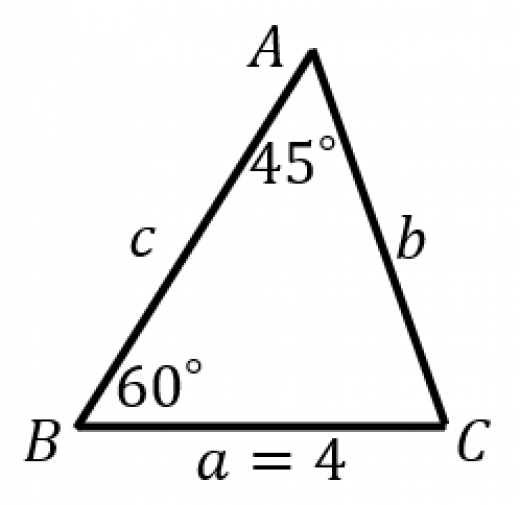

 の定義より,
の定義より,
















