1の三乗根オメガを用いた計算と因数分解
更新
の三乗根 (オメガ)に関する話題です。
1の三乗根
1の三乗根
1の三乗根,つまり3乗して1になる数を考えてみます。
を変形すると,
因数分解すると,
つまり, または になります。後者の二次方程式を解くと, になります。
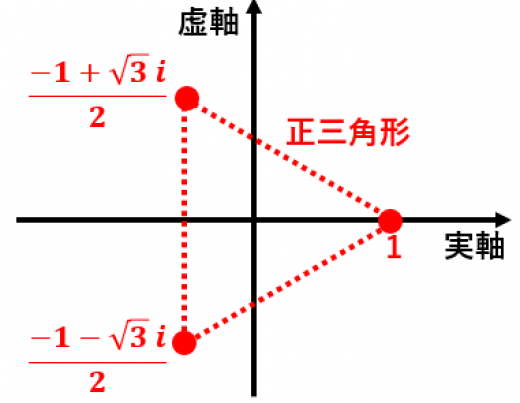
つまり,1の三乗根は の つです。3つのうち2つは虚数です。複素数平面で1の三乗根を図示すると,正三角形になります。
オメガとは
オメガとは
1の三乗根のうち虚数のものを と表すことが多いです。虚数のものは2つありますが,そのうちの一方を とおくと,もう一方は になります。
実際,以下が成立します:
つまり,どちらを とおいても1の3乗根は の3つになります。
オメガに関する基本的な性質
オメガに関する基本的な性質
-
は1の三乗根なので, は当然成立します。 -
さきほど見たように は の解なので が成立します。 -
簡単な計算でも,複素数平面における考察でもわかります。
ちなみに,二次方程式を解く際に虚数単位 が必要になったのと同様に,三次方程式を解く際に が必要になります。→カルダノの公式と例題【三次方程式の解の公式】
オメガの多項式を計算する問題
オメガの多項式を計算する問題
の多項式は必ず という形まで計算できる。特に試験問題では となる場合が圧倒的に多い。
まず を用いて の二次式まで計算します。次に を用いて一次式にします。
この方法でどんな多項式にも対応できます。
オメガを含む式の「有理化」
を「有理化」してみましょう。
となるので, と表される。
余談:大学数学の内容ですが,これは が体になることを意味します。
オメガを用いた因数分解
オメガを用いた因数分解
本記事のメインテーマです。
の多項式 が を因数に持つ必要十分条件は なのでさきほどの計算方法を用いて簡単に確認できる。
特に, のような形のときに効果てきめんです。
を因数分解せよ。
簡単に因数分解できなさそうですが, であり,同様に も分かるので は を因数に持ちます。あとは頑張って割り算をするのみ:
→高校数学の問題集 ~最短で得点力を上げるために~ のT28では,オメガを用いずに頑張って因数分解する方法も紹介しています。
次は2003年京大前期の第四問です。
は で割り切れるか。
同様に かどうか確認するだけです。
も同様にして となることが分かるので は で割り切れる!
の係数が全部 であるような多項式が出てきたら を意識するようにしましょう。
Tag:複素数の美しい性質と効果まとめ










