共役複素数の覚えておくべき性質
複素数 に対して, のことを共役な複素数と言います(ただし は実数)。
例えば, に対して共役な複素数は です。
この記事では「複素数の共役」の意味と関連する性質を解説します。
共役複素数の意味
共役複素数の意味
複素数 に対して, のことを共役な複素数と言います(ただし は実数)。
共役は「きょうえき」ではなく「きょうやく」と読みます。複素数 の共役複素数を と書くことが多いです。
- の共役複素数は
- の共役複素数は
- の共役複素数は (虚部だけをマイナスにするので,実数 の共役複素数は 自身です)。
共役な複素数は,
- 「虚部をマイナス1倍したもの」と言うこともできます。
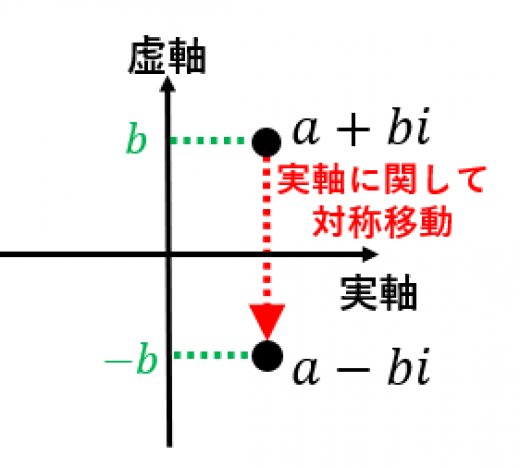
- 「複素数平面上で実軸に関して対称移動させたもの」と言うこともできます。
共役複素数の基本的な性質
共役複素数の基本的な性質
任意の複素数 に対して,
つまり「共役」を2回とると元に戻ります。実際, の共役複素数は で,その の共役複素数は でもとに戻ります。
任意の複素数 に対して,
「共役」と「足し算」の順番は交換できるという性質です。実際,, とおき計算すると,
となります。同様に,引き算・かけ算・割り算についても以下の性質を確認できます。
任意の複素数 に対して,
- (ただし )
共役複素数と絶対値
共役複素数と絶対値
任意の複素数 に対して, は0以上の実数。
例えば, とその共役な複素数 の積は,
となります。
より一般に, と の積は,
となります。 は の絶対値と呼ばれ と書くことが多いです。つまり, という式が成立します。
この性質は,分母に複素数が含まれている場合の実数化をはじめ,複素数が絡む多くの問題で用いられます。基本的な公式ですが,非常に重要です。
共役複素数と方程式の解
共役複素数と方程式の解
実数係数多項式 という方程式に関して, が解なら も解である。
非常に重要な性質です。導出方法も合わせて覚えておくと良いでしょう。
2次方程式 において,複素数 が解なら も解になります。これは解の公式からすぐにわかります(ただし, は実数)。
3次方程式の場合に上の「重要な性質」を適用してみると,実数係数の3次方程式は,3つの解が全て実数,または (ただし, は実数)と表せることがわかります。頻出です。
それでは「重要な性質」を証明します。 知らないと思いつくのは難しい証明です。
実数係数の 次方程式 に対して, が解のとき, となる。両辺の共役複素数をとって,
ここで「共役」と「足し算」は順番を交換できるので,
さらに「共役」と「かけ算」は順番を交換できるので,
最後に, は実数なので を用いる:
これは がもとの方程式の解であることを表している。
証明の途中で の共役複素数が であることを用いているので実数係数という条件は必須です。
余談
-
有理数係数の方程式に関しても似たような定理が成立します。→共役無理数に関する二つの定理
-
共役複素数も方程式の解になるという性質は東大2019年大問6で効いてきます。
-
→高校数学の問題集 ~最短で得点力を上げるために~のT122でも,この証明を紹介しています。
ちなみに大学の数学では,複素ベクトル空間の標準内積を定義するときに自然に共役複素数が登場します。
Tag:複素数の美しい性質と効果まとめ











