平面の方程式とその3通りの求め方
座標平面における直線は
という形で表せる。
同様に,
座標空間上の平面の方程式は
という形で表せる。
平面の方程式の例
平面の方程式の例
例えば,座標空間上で という一次式を満たす点 の集合はどのような図形を表すでしょうか?
実は,この式を満たす点の集合は平面になります。
この記事では,実際に という3点を通る平面の方程式を計算し,答えが
になることを確認してみます。
平面の方程式を求める例題
平面の方程式を求める例題
3点 を通る平面の方程式を計算せよ。
通る3点が与えられたときに,その平面の方程式を求める方法を3通り紹介します。
- ベクトルの外積と法線ベクトルを用いる方法
- 連立方程式を解く方法
- ベクトル方程式を用いる方法
1:外積と法線ベクトルを用いる方法
1:外積と法線ベクトルを用いる方法
レベルは高いですが3つの中で最も計算が単純な方法です。
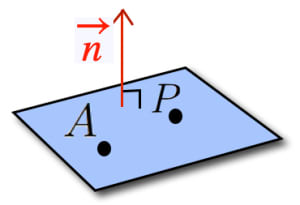
平面内のベクトルは全てある定ベクトルと垂直になります。そのような定ベクトルを法線ベクトルと言います。法線ベクトルの1つを とします。平面上の任意の一点を とすると,
点 が求める平面上にある
と法線ベクトル が垂直
となります。これが求める平面の方程式です。よって,法線ベクトルを求めればよいわけです。
法線ベクトルは, に垂直なベクトルで,これはベクトルの外積を用いれば一瞬で求められます。→ベクトルの内積と外積の意味と嬉しさ
より法線ベクトルは,
よって,求める平面の方程式は,
これを整理して,
2:連立方程式を解く方法
2:連立方程式を解く方法
平面上の直線の方程式は,通る2点を代入して連立方程式を解くことで求められました。それと同様に,通る3点を代入することで平面の方程式を求められます(空間の性質は平面の場合の手法を一般化できないか考えるべし)。
上記の例のように未知数が4つで方程式は3つなので,連立方程式の解は1つに決まりません。 を定数と見て について解き,最後に で割って整理しましょう。
に通る3点の値を代入して,
これを解いて,
よって求める平面の方程式は,
つまり,
3:ベクトル方程式を用いる方法
3:ベクトル方程式を用いる方法
平面上の任意の点 は,実数 を用いて,
と表せます。始点を原点に直すと,
この形でも平面の方程式を表せているので答えになっています。 の形に直したいときには,連立方程式を解いて を消去しないといけないので少しめんどうです。
とおくと,上記の公式より
これを整理して を消去すると,
(この例の場合は を消去するのがよい)
平面の方程式の一般形
平面の方程式の一般形
今までは具体例を考えていましたが,より一般に,
という一次式を満たす点の集合は平面になります。
実際,上記の方法1を見直してみると,
は,法線ベクトルが であるような平面の方程式を表していることが分かります。
→高校数学の問題集 ~最短で得点力を上げるために~のT105では,この記事の復習ができます。計算ミスを減らすコツも紹介しています。
どの方法でも良いので高速で計算できるようになっておきましょう!
Tag:有名な定理を複数の方法で証明











