ベータ分布の意味と平均・分散の導出
ベータ分布とは,確率密度関数が
であるような確率分布のことです。
ただし, はパラメータ(正の実数)であり, は規格化定数です。
ベータ分布の意味
ベータ分布の意味
ベータ分布は「コイン投げにおける表が出る確率の予測分布」という解釈ができます。
表が出る確率 が不明であるコインを何回か投げて,表が 回,裏が 回出たとします。このとき「表が出る確率の予測値」は,パラメータが であるベータ分布に従うと考えることができます(→注)。
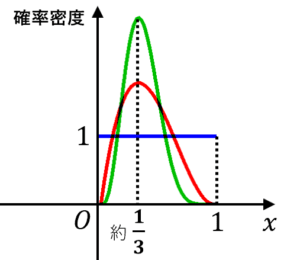
例えば,
のときは,ベータ分布は青い直線のように一様分布になります。つまり, のとき(そもそもコインを投げていないとき)は「情報が全く無いので, は一様分布に従う」と解釈できます。
のときは,ベータ分布は赤い曲線のようになります。つまり, のときは「表が出る確率は に近そうだけど,試行回数が少ないので, からは遠い値かもしれない」と解釈できます。
のときは,ベータ分布は緑の曲線のようになります。つまり, のときは「表が出る確率は に近そうで,さきほどより試行回数が多いので,より自信を持って に近いと言える」と解釈できます。
注:上記は大雑把な説明です。より正確に言うと, 事前分布を一様分布とし,尤度が二項分布(コイン投げ)であるときの事後分析がベータ分布になります。
ベータ分布のパラメータ
ベータ分布のパラメータ
ベータ分布は, という2つのパラメータを持っています。 の値によって分布の形は大きく異なります。Wolfram Alphaでbetadistribution[a,b]と入力すればパラメータが のベータ分布の確率密度関数のグラフを見ることができます。 や をいろいろな値にして図示してみると楽しいです。
例えば, の場合,確率密度関数は に関して対称になります。
ベータ分布の規格化定数
ベータ分布の規格化定数
ベータ分布の平均
ベータ分布の平均
ベータ分布の平均は です。これは綺麗なので覚えておいてもよいでしょう。
ベータ分布の分散
ベータ分布の分散
ベータ分布の分散は です。これは覚える必要はありません。
分散は,
第一項はさきほどと同様にベータ関数の積分公式を用いて計算できる。上式は,
となる。
なお,コイン投げはベルヌーイ分布(確率1/2ずつで を取る分布)またはラーデマッハー分布(Rademacher 分布,確率1/2ずつで を取る分布)で表されることが多いです。











