三角関数の合成のやり方・証明・応用
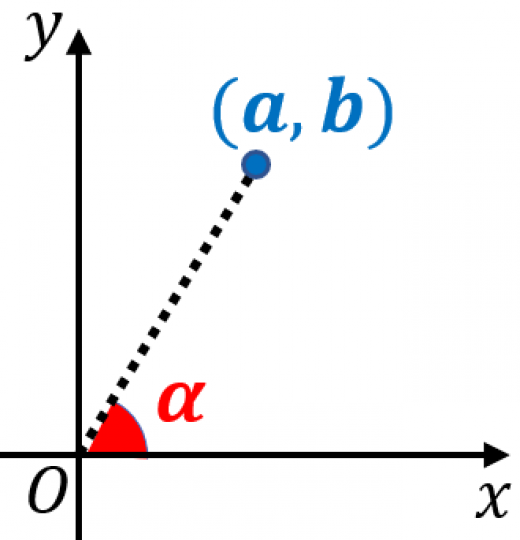
ただし, は図のように に対応する角度。つまり「 軸の正の部分を反時計回りにいくら回転したら を通るか」を表す角度。
三角関数の合成について,証明・意味・応用例をわかりやすく整理しました。
合成公式の証明(sinによる合成)〜加法定理の逆〜
合成公式の証明(sinによる合成)〜加法定理の逆〜
と の足し算を だけの式,あるいは だけの式にすることを「合成」と言います。
まず三角関数の合成公式を証明してみます。ここではsinに合成する公式を証明します。
加法定理:
を使って右辺を展開するのみです。
の加法定理より,合成公式の右辺は,
ここで, は に対応する下図のような角度であったので
,

これらを上式に代入すると,
となり,三角関数の合成公式の左辺になった。
証明からもわかるように,三角関数の合成は加法定理の逆の操作と言えます。
よって 「 という式を見たときに,加法定理を逆に使えば合成公式は導けるので覚える必要はない」という人もいるでしょう。
しかし,合成公式は頻繁に使うので 時短のためにも から を求める方法を覚えるのがオススメです。
cosによる合成公式
cosによる合成公式
「サインで合成する」公式だけでなく「コサインで合成する」公式もあります:
ただし, は , を満たす角度。
コサインの場合は, から角度 を求めるのが難しいです。少しめんどうですが加法定理の逆の操作で合成していきましょう。
加法定理より,合成公式の右辺を変形すると
となり,合成公式の左辺となった。
cosによる合成公式の補足
- cosによる合成公式は覚える必要はありません。
- 「サインでできることはコサインでもできる」という認識は重要です。
- コサインバージョンは,コサインの加法定理を使って証明できます。また,サインの合成公式において位相をズラすことでも証明できます( を使う)。
三角関数の合成の例
三角関数の合成の例
実際に三角関数を合成してみましょう。
sinの形に合成する
をサインに合成せよ。
として三角関数の合成公式
を使うと,
となる。ただし, は に対応する角度,つまり の直角三角形の内角であり,

つまり
このように,サインに合成する場合,図を描くのがわかりやすいです。
cosの形に合成する
コサインに合成することもできます。 コサインの場合は, から角度 を求めるのが難しいです。少しめんどうですが加法定理の逆の操作で合成していきましょう。
をコサインに合成せよ。
よって, となる を見つければ,上式は
となる。そして,そのような は例えば とすればよい。つまり,
応用例1
応用例1
三角関数の合成は,関数のグラフを描くのに役立つことがあります。
のグラフの概形を描け。
三角関数の合成公式より,図を用いて求めると

よって,描きたい関数は のグラフを 軸方向に 平行移動したもの。

応用例2
応用例2
三角関数の合成公式を使うと「」という扱いにくい関数をサイン(を平行移動したもの)という分かりやすい関数に変形できます。
そのため,以下の例題のように,関数の最大値や最小値を計算しやすくなります。
が実数全体を動くとき, の最大値,最小値を求めよ。
三角関数の合成公式より,
ただし, は に対応する角度(具体的に求める必要はない)。
よって の最小値は ,最大値は である。
→高校数学の問題集 ~最短で得点力を上げるために~のT11では,本問の3通りの解法を紹介しています。
cosへの合成はほとんど使った記憶がないです。











