ヤングの不等式の3通りの証明
更新
のとき, 等号成立条件は
シンプルで美しい不等式です。
ヤングの不等式の証明
ヤングの不等式の証明
3通りの証明を紹介します。
1:積分を用いて図形的に証明する方法
一般形である「積分形のヤングの不等式」を示します。
まず, を示す。ただし, は を満たす単調増加関数で, はその逆関数(これを積分形のヤングの不等式と言う)。
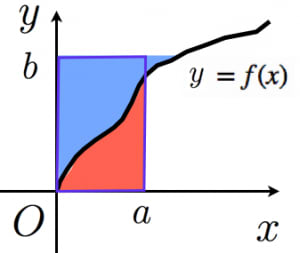
左辺第一項は赤い部分の面積。左辺第二項は青い部分の面積。右辺は紫の長方形の面積より不等式が成立。
ここで, とおくと, より逆関数は となる。
よって, などにより,積分形のヤングの不等式から「もとのヤングの不等式」が得られる。
なお,逆関数の求め方については逆関数の3つの定義と使い分けを参照してください。
この証明に関する入試問題も頻出です。
2:イェンゼンの不等式を用いる方法
係数の和が なのでイェンゼンの不等式が使えそうな形です。
とおくと, より は凸関数である。よってイェンゼンの不等式より,
つまり, である。
ここで, とおくとヤングの不等式を得る。
3:重み付き相加相乗平均の不等式を用いる方法
係数の和が なので重み付き相加相乗平均の不等式も使えそうです。
重み付き相加相乗平均の不等式: において,
, とおくとヤングの不等式になる。
つまり, ヤングの不等式は重み付き相加相乗平均の不等式の特殊形とみることもできます。
関連する不等式
関連する不等式
-
のとき,ヤングの不等式は となり相加相乗平均の不等式と一致します。
-
ヤングの不等式は,ヘルダーの不等式など,他の不等式の証明で活躍します。→ミンコフスキーの不等式とその証明
積分形のヤングの不等式
証明1で登場した以下の「積分形のヤングの不等式」もおさえておきましょう。
単調増加な連続関数 とその逆関数 において, のとき, が成立する。
「積分形のヤングの不等式」で とすれば「もとのヤングの不等式」が得られます。
積分を用いた導出はなかなか美しいです。











